Математика в 4 классе

Ответы к стр. 96-97

1. Назови знакомые тебе геометрические фигуры, начерти их в тетради и обозначь буквами.

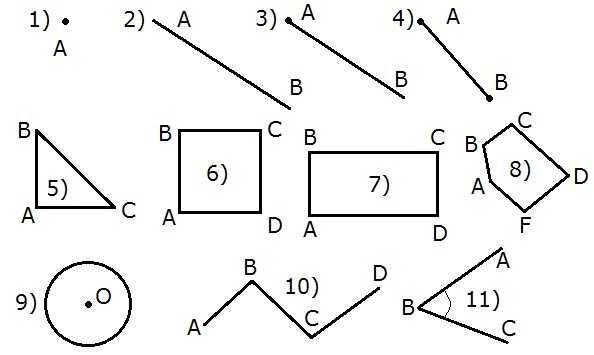
1) Точка А; 2) Прямая АВ; 3) Луч АВ; 4) Отрезок АВ; 5) Треугольник АВС; 6) Квадрат ABCD; 7) Прямоугольник ABCD; Многоугольник ABCDF; 9) Окружность; 10) Ломанная ABCD; 11) Угол ABC.

2. Что ты знаешь о многоугольниках? Сколько вершин, углов и сторон у двенадцатиугольника?

Многоугольники называются по числу углов. Если в многоугольнике 3 угла — это треугольник, если 4 — это четырехугольник, если 5 — пятиугольник.
В любом многоугольнике число углов равно числу сторон и вершин.
В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.

3. Какие виды треугольников ты знаешь? Может ли прямоугольный треугольник быть равносторонним? разносторонним? Может ли тупоугольный треугольник быть равнобедренным? Начерти в тетради равнобедренный прямоугольный треугольник.

Треугольники, от вида углов, бывают остроугольные, тупоугольные и прямоугольные. В зависимости от длин сторон треугольники бывают разносторонними, равносторонними, равнобедренными.
Прямоугольный треугольник не может быть равносторонним, но может быть разносторонним или равнобедренным.
Тупоугольный треугольник может быть равнобедренным.В треугольнике АВС угол ВАС прямой, а стороны АВ и АС равны между собой.

В треугольнике АВС угол ВАС прямой, а стороны АВ и АС равны между собой.

4. Какие виды четырёхугольников ты знаешь? Продолжи предложения:
1) Прямоугольник — это такой четырёхугольник, у которого … .
2) Квадрат — это такой прямоугольник, у которого … .

Прямоугольник, квадрат.
1) Прямоугольник — это четырехугольник, у которого все углы прямые, а противоположные стороны равны между собой.
2) Квадрат — это прямоугольник, у которого все углы прямыеу и все стороны равны.

5. 1) Среди четырёхугольников, изображённых на рисунке 1, найди прямоугольники и запиши их названия; подчеркни название квадрата.
2) Найди периметр прямоугольника ОРКС и площадь квадрата. Объясни, почему четырёхугольник ABCD нельзя назвать квадратом.

1) ОРКС, FKMЕ, EKМD.
2) Периметр прямоугольника ОРКС равен: 15 • 2 + 9 • 2 = 48 (мм).
Площадь квадрата FKMЕ равна: 9 • 9 = 81 (мм2).
Четырехугольник ABCD нельзя назвать квадратом, так как он не прямоугольник — в нём нет прямых углов.

6. Определи вид каждого треугольника, если его периметр находят так:
1) 3 + 4 + 5 = 12 (см);      2) 3 • 2 + 4 = 10 (см);     3) 5 • 3 = 15 (см).

1) разносторонний треугольник;
2) равнобедренный треугольник;
3) равносторонний треугольник.

7. Рассмотри рисунок 2 на полях и запиши названия всех прямоугольных, остроугольных и тупоугольных треугольников; подчеркни названия равнобедренных треугольников.

Прямоугольные треугольники: ABO, ВСК, ВОК, CDO.
Остроугольные треугольники: AOD.
Тупоугольные треугольники: АКО, CDK, СОК.

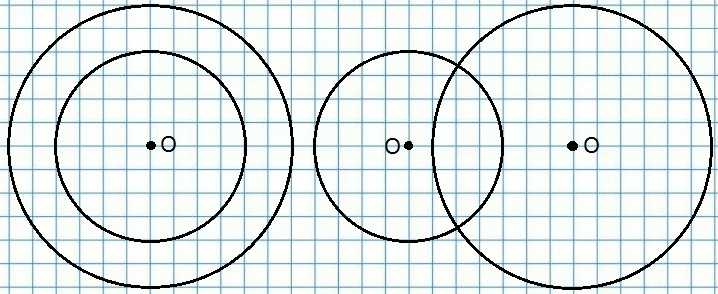
8. Начерти 2 окружности с радиусами 2 см и 3 см сначала с общим центром, а потом с разными центрами.

9. Найди длину ломаной АОКС (рис. 2, задание 7).

Длина ломанной АОКС равна: 30 + 30 + 40 = 100 мм = 10 см

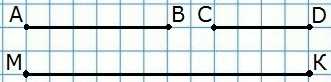
10. Начерти 3 отрезка: отрезок АВ длиной 3 см, отрезок CD, который на 1 см короче отрезка АВ, и отрезок МК, который в 2 раза длиннее отрезка АВ. Во сколько раз отрезок CD короче отрезка МК?

CD =  3 – 1 = 2 (см)
МК = 3 х 2 = 6 (см)
МК CD = 6 2 = 3 раза

11. Начерти любой прямоугольник и найди его площадь и периметр.

Периметр прямоугольника ABCD равен: (4 + 2) • 2 = 12 см, а площадь: 4 • 2 = 6 см2

12. Участок квадратной формы обнесён с трёх сторон забором, длина которого 90 м. Чему равна площадь этого участка?

1) 90 3 = 30 (м) — длина стороны участка
2) 30 • 30 = 900 (м2)
О т в е т: площадь участка 900 м2.

← Предыдущая

Следующая →

Класс математика и конструирование

Уроки математики и конструирования во 2 классе представляют собой важную часть обучения, направленную на развитие логического мышления и способности анализировать пространственные формы.

Одной из ключевых тем в программе класса является изучение фигур и их свойств. Ученикам предлагается различать и распознавать треугольники и четырехугольники. Это помогает детям развивать внимательность, точность и наблюдательность.

На практике, ученикам предлагается рисовать и конструировать треугольники и четырехугольники используя ручки, линейки и геометрические шаблоны. Также есть возможность использовать игровые материалы, такие как пазлы или кубики, для формирования и тренировки пространственного мышления.

Ученикам предлагается сравнивать и классифицировать различные фигуры по количеству сторон и углов, и определять их основные характеристики. Таким образом, класс математика и конструирование помогает развивать ключевые навыки и умения, необходимые для успешного обучения и понимания геометрии в будущем.

Треугольники	Четырехугольники
Равносторонний	Прямоугольник
Равнобедренный	Параллелограмм
Разносторонний	Ромб

Сколько треугольников на рисунке 1 класс с ответами

Страница 96

1. Имеются 8 коробочек и 5 шариков. На сколько коробочек больше, чем шариков? Ответ: 8 — 5 = 3 коробочки — больше, чем шариков

2. Реши задачи, используя вычитание. Задача 1. В хозяйстве 10 кур и 6 уток. На сколько уток меньше, чем кур? Задача 2. Сшили 5 костюмов и 12 платьев. На сколько платьев больше, чем костюмов? Ответ: Задача 1. 10 — 6 = 4 утки — меньше, чем кур Задача 2. 12 — 5 = 7 платьев — больше, чем костюмов

3. На сколько: 3 меньше 5; 10 больше 6; 8 больше 6; 4 меньше 13? Ответ: 5 — 3 = 2 3 меньше 5 на 2

8 — 6 = 2 8 больше 6 на 2

10 — 6 = 4 10 больше 6 на 4

13 — 4 = 9 4 меньше 13 на 4

Страница 97

4. Сравни числа. На сколько первое число больше или меньше второго? 13 и 6 10 и 6 7 и 10 0 и 7 Ответ: 13 и 6 13 — 6 = 7 13 больше 6 на 7

7 и 10 10 — 7 = 3 7 меньше 10 на 3

10 и 6 10 — 6 = 4 10 больше 6 на 4

0 и 7 7 — 0 = 7 7 больше 0 на 7

5. На сколько число 10 больше каждого из чисел 3; 5; 2; 6? Ответ: 10 — 3 = 7 10 больше 3 на 7

10 — 5 = 5 10 больше 5 на 5

10 — 2 = 8 10 больше 2 на 8

10 — 6 = 4 10 больше 6 на 4

6. Составь все предложения о парах чисел. Ответ: Двенадцать меньше восемнадцати. Восемнадцать больше двенадцати.

Ноль меньше одного. Один меньше двух. Ноль меньше двух. Один больше нуля. Два больше одного. Два больше нуля.

7. Сравни числа. Сделай рисунки, используя красные и синие стрелки. 10 и 6 9 и 15 17 и 6 8 и 14 Ответ:

8. Используя результаты сложения, выскажи предположения о результатах вычитания с теми же числами. 6 + 9 = 15 7 + 4 = 11 15 — 6 11 — 7 15 — 9 11 — 4 Проверь своё предположение: выполни вычитание. Ответ: 6 + 9 = 15 — первое слагаемое (6) плюс второе слагаемое (9) равно сумма (15). 15 — 6 = 9 — так как, если из суммы (15) вычесть первое слагаемое (6), то получится второе слагаемое (9). 15 — 9 = 6 — так как, если из суммы (15) вычесть второе слагаемое (9), то получится первое слагаемое (6).

7 + 4 = 11 — первое слагаемое (7) плюс второе слагаемое (4) равно сумма (11). 11 — 7 = 4 — так как, если из суммы (11) вычесть первое слагаемое (7), то получится второе слагаемое (4). 11 — 4 = 7 — так как, если из суммы (11) вычесть второе слагаемое (4), то получится первое слагаемое (7).

9. Врач принял семерых больных. В коридоре ждут своей очереди ещё трое. Сколько человек пришло к врачу? Ответ: 7 + 3 = 10 человек — пришло к врачу

Страница 98

10. Мастер собрал 4 таких велосипеда. Сколько колёс ему потребовалось? Ответ: На рисунке у велосипеда 3 колеса, т.е. на один велосипед требуется 3 колеса. Значит, чтобы собрать 4 велосипеда, мастеру потребовалось: 4 • 3 = 12 колес

11. Проанализируй форму, цвет и расположение фигур. Назови три следующие фигуры. Ответ: Фигуры располагаются в следующей последовательности: Синий квадрат, красный круг, зеленый треугольник, желтый треугольник, синий квадрат, красный круг, зеленый треугольник, желтый треугольник, синий квадрат, красный круг. Следующие три фигуры: зеленый треугольник, желтый треугольник, синий квадрат.

12. Какие многоугольники ты видишь на рисунках? Ответ: 1 рисунок: шестиугольники. 2 рисунок: пятиугольники.

13. Выскажи предположение о длине кружева. Проверь своё предположение: выполни измерение. Ответ:

Страница 99

14. Сколько стёкол нужно вставить во все рамы? Ответ: Если всего 4 рамы и в каждую раму нужно вставить по 2 стекла, то во все рамы нужно вставить 4 • 2 = 8 стекол

15. Цена ручки 4 р. Какова стоимость двух ручек? Сколько сдачи даст кассир с 10 р., если купить одну ручку; две ручки? Ответ: 1) 4 • 2 = 8 р. — стоимость двух ручек 2) 10 — 4 = 6 р. — сдача, если купить одну ручку 3) 10 — 8 = 2 р. — сдача, если купить две ручки

16. Прочитай условие задачи. Придумай вопрос и реши задачу. У Толи 12 машинок, а у Вадима на 4 машинки меньше. Ответ: Вопрос: Сколько машинок у Вадима? 12 — 4 = 8 машинок

17. Сколько всего треугольников на рисунке? Найди верный ответ среди данных чисел. Ответ: На рисунке всего 8 треугольников.

18. Проверь работу «машин». Какая из них требует ремонта? Ответ: 5 — 4 = 1 12 — 3 = 9 13 — 4 = 9 13 — 3 = 10 12 — 4 = 8 11 — 3 = 8 11 — 4 = 6 — неверно 3 — 0 = 3

Как найти треугольники?

Для нахождения треугольников на рисунке необходимо проанализировать его геометрическую структуру. Вот несколько шагов, которые помогут вам в этом:

1. Визуализируйте все отрезки на рисунке, соединяющие две точки. Убедитесь, что каждый отрезок соответствует некоторому ребру треугольника.
2. Проверьте каждую тройку отрезков на то, являются ли они сторонами треугольника. Для этого необходимо убедиться, что выполняются следующие условия:
   • Сумма длин любых двух сторон треугольника больше длины третьей стороны.
   • Сумма углов треугольника равна 180 градусам.
3. Отметьте все найденные треугольники на рисунке, чтобы сохранить результаты вашего анализа.

Помните, что на рисунке может быть разное количество треугольников, в зависимости от его сложности и стиля рисования

При визуальном поиске треугольников всегда акцентируйте внимание на геометрических формах и углах, которые они создают

Не забывайте практиковаться и развивать свои навыки в анализе геометрических фигур!

Количество четырехугольников на рисунке

На рисунке представлены различные геометрические фигуры, включая треугольники и четырехугольники. Чтобы определить количество четырехугольников, нужно внимательно исследовать фигуры на рисунке и сосчитать все, у которых есть четыре стороны и четыре угла.

Фигура	Описание
Прямоугольник	Четырехугольник с противоположными сторонами, образующими прямой угол.
Квадрат	Прямоугольник, у которого все стороны равны.
Ромб	Четырехугольник с равными сторонами.
Трапеция	Четырехугольник с двумя параллельными сторонами.

Теперь можно приступить к подсчету. На рисунке обнаружены:

• 2 прямоугольника
• 1 квадрат
• 1 ромб
• 3 трапеции

Общее количество четырехугольников на рисунке равно 7.

Зная классификацию и характеристики четырехугольников, можно легко идентифицировать их на рисунках и в реальной жизни, что помогает в учебе и практическом применении математики и конструирования.

Разновидности визуальных задач

Визуальные задачи позволяют развивать у детей наблюдательность, логическое мышление и умение анализировать информацию. Они могут содержать разнообразные диаграммы, графики, рисунки или числовые ряды.

Одной из разновидностей визуальных задач являются задачи на поиск различий. В таких задачах детям предлагается найти отличия между двумя или несколькими изображениями. Это способствует развитию внимания, умению сравнивать и сопоставлять объекты, а также находить взаимосвязи.

Задачи на счет представляют собой графическую форму отображения числовых значений. Детям необходимо сосчитать количество предметов, представленных на рисунке, и выбрать правильный ответ из вариантов.

Разновидность задачи	Описание
Задачи на поиск различий	Задачи, в которых необходимо найти отличия между двумя или несколькими изображениями
Задачи на счет	Задачи, в которых необходимо сосчитать количество предметов на рисунке
Головоломки на логику

Визуальные задачи являются не только увлекательными, но и полезными для развития различных когнитивных навыков у детей

Постепенно увеличивая сложность задач, можно помочь детям развить логическое мышление, внимание и наблюдательность, а также улучшить их способности к анализу и решению проблем

Проверка наличия внутренних отрезков

При подсчете количества отрезков на рисунке следует учитывать только такие отрезки, которые находятся внутри треугольников.

Для определения внутренних отрезков следует рассмотреть каждый отрезок на рисунке и проверить, лежит ли он внутри какого-либо треугольника. Для этого можно воспользоваться следующим алгоритмом:

1. Для каждого треугольника на рисунке:
   1. Проверить, лежит ли начало отрезка внутри треугольника с помощью формулы для определения нахождения точки внутри треугольника;
   2. Проверить, лежит ли конец отрезка внутри треугольника;
   3. Если и начало, и конец отрезка лежат внутри треугольника, то он является внутренним отрезком;
2. Подсчитать количество внутренних отрезков.

Этот алгоритм позволит нам точно определить, какие отрезки являются внутренними на рисунке и посчитать их количество.

Виды треугольников и их количество на каждом рисунке в 4 классе

В четвертом классе на уроках геометрии ученики изучают треугольники и их свойства. Одной из задач на уроке может быть подсчет количества треугольников на каждом рисунке

При этом важно помнить, что не все треугольники на рисунке могут быть уникальными, некоторые могут быть равными или подобными

Основные виды треугольников, которые ученики могут встретить на рисунке, включают равносторонний, равнобедренный и разносторонний треугольники.

Равносторонний треугольник имеет три равные стороны и три равных угла. Он обозначается как ТР. Для определения количества равносторонних треугольников на рисунке, следует искать все треугольники, у которых все три стороны равны.

Равнобедренный треугольник имеет две равные стороны и два равных угла. Он обозначается как ТР_{равнобедр}. Для определения количества равнобедренных треугольников на рисунке, следует искать все треугольники, у которых две стороны равны.

Разносторонний треугольник не имеет равных сторон и равных углов. Он обозначается как ТР_{разностор}. Для определения количества разносторонних треугольников на рисунке, следует искать все треугольники, у которых все три стороны разные.

Подсчет количества треугольников на рисунке проводится путем нахождения каждого треугольника и классификацией его по виду: равносторонний, равнобедренный или разносторонний. В итоге получается количество треугольников каждого вида на рисунке.

Отслеживание пересечений и прямоугольных треугольников

При анализе рисунка и подсчете количества треугольников и отрезков следует обратить внимание на пересечения между фигурами и наличие прямоугольных треугольников. Пересечения могут быть встречены как между отрезками, так и между треугольниками

Для выявления пересечений между отрезками можно использовать методы геометрии, например, проверку на пересечение отрезков. Если два отрезка пересекаются, значит, между ними можно провести еще один треугольник. Следует учесть, что пересечения могут быть как внутри, так и снаружи другой фигуры, поэтому необходимо учитывать все возможные варианты

Пересечения могут быть встречены как между отрезками, так и между треугольниками. Для выявления пересечений между отрезками можно использовать методы геометрии, например, проверку на пересечение отрезков. Если два отрезка пересекаются, значит, между ними можно провести еще один треугольник. Следует учесть, что пересечения могут быть как внутри, так и снаружи другой фигуры, поэтому необходимо учитывать все возможные варианты.

Также стоит обратить внимание на прямоугольные треугольники. Прямоугольные треугольники имеют угол в 90 градусов, что делает их уникальными

Для определения прямоугольных треугольников можно использовать теорему Пифагора или другие методы, позволяющие определить соотношение длин сторон треугольника.

В результате анализа рисунка и применения соответствующих методов можно определить количество треугольников и отрезков, а также выделить прямоугольные треугольники. При этом следует учесть все возможные варианты пересечений и углы треугольников, чтобы исключить возможность пропустить какой-либо элемент.

Количество треугольников в зависимости от количества сторон

Определение количества треугольников на рисунке может быть интересным и познавательным упражнением для учеников 4 класса. Это помогает развить логическое мышление и способность анализировать геометрические фигуры.

Чтобы посчитать количество треугольников на рисунке, необходимо обратить внимание на количество сторон каждой фигуры. Треугольник состоит из трех сторон, поэтому нужно найти все треугольники, учитывая различные комбинации сторон на рисунке

Если на рисунке есть фигура с 3 сторонами, то это уже один треугольник. Если есть фигура с 4 сторонами, то можно найти дополнительные треугольники, соединив вершины этой фигуры. Например, если есть четырехугольник ABCD, то мы можем найти 2 дополнительных треугольника ABC и ACD.

Если на рисунке есть фигура с 5 сторонами, то можно найти еще больше треугольников, соединив различные вершины. Например, если есть пятиугольник ABCDE, то мы можем найти 3 дополнительных треугольника ABC, ABD и ACD.

Таким образом, количество треугольников на рисунке зависит от общего количества сторон на фигурах. Чем больше фигур и сторон, тем больше треугольников можно найти.

Учителя могут давать различные задания, чтобы ученики могли попрактиковаться в поиске треугольников на рисунках. Например, можно дать рисунок с фигурами и попросить учеников посчитать количество треугольников или даже попросить их нарисовать собственный рисунок с фигурами и посчитать количество треугольников на нем.

Такая задача не только развивает навыки работы с геометрическими фигурами, но и помогает ученикам развивать наблюдательность, логическое мышление и умение анализировать информацию.

Историческая справка

Геометрия, как и другие науки, возникла из потребностей практики. Само слово «геометрия» греческое, в переводе означает «землемерие». Люди очень рано столкнулись с необходимостью измерять земельные участки. Это требовало определённых знаний и умений. Начав с прямоугольников и треугольников, постепенно начали измерять и изучать свойства более сложных геометрических фигур.

По дошедшим до нас египетским папирусам и древневавилонским текстам видно, что уже за 2 тысячи лет до нашей эры люди умели определять площади треугольников, прямоугольников, трапеций, приближенно вычислять площадь круга. Они знали также формулы для определения объёмов куба, цилиндра, конуса, пирамиды и усеченной пирамиды. Сведения по геометрии вскоре стали необходимы не только при измерении земли.

Сейчас геометрия – один из важнейших разделов математики. Конечно, она занимается не только измерением площадей. Мы будем относить в этот раздел задачи, так или иначе связанные с линиями на плоскости и в пространстве. Геометрические знания очень нужны художникам и архитекторам, проектировщикам дорог и космических кораблей. Да и любому человеку не помешает хорошее пространственное воображение.

В данном занятии мы познакомимся с некоторыми геометрическими фигурами, будем развивать геометрическое видение рисунка. У некоторых людей пространственное видение развито от природы очень хорошо, они в уме могут решать геометрические задачи, играть вслепую в шахматы, ориентироваться на местности. Не у всех это есть с рождения. Геометрические задания помогут развить такое воображение.

Начнем с самого начала – с геометрических объектов.

Сложная задачка для первоклашек про треугольники: с ней не всегда могут справиться взрослые. Проверьте свои силы

Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).

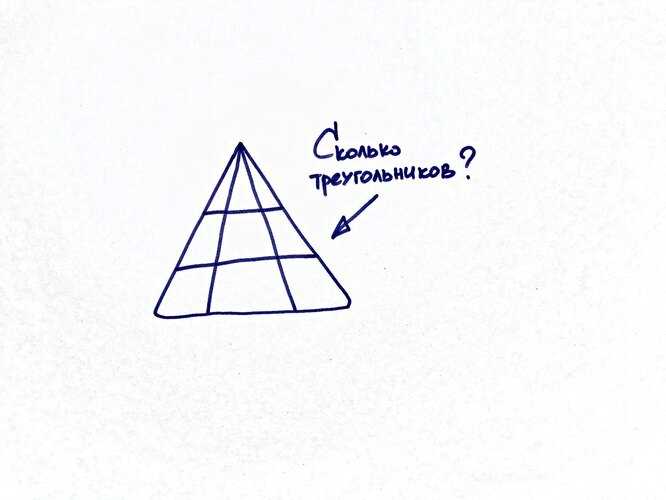
Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.

Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.

Основная информация о математике в 4 классе

В четвертом классе ученики начинают изучать основы математики, которые будут полезны им в дальнейшем. Курс математики в этом классе включает такие темы, как:

• Сложение и вычитание двузначных и трехзначных чисел;
• Умножение и деление чисел до 100;
• Сравнение и упорядочивание чисел;
• Работа с таблицами и диаграммами;
• Измерение длин, массы и времени;

Важной частью курса является также работа с геометрическими фигурами. В четвертом классе ученики изучают такие понятия, как треугольники, прямоугольники, квадраты и круги

Учащиеся учатся опознавать, классифицировать и строить эти фигуры.

Курс математики в четвертом классе также включает работу с задачами на логику и решение уравнений с неизвестными числами. Ученики учатся анализировать и решать разнообразные математические задачи, развивая свои логическое и аналитическое мышление.

Изучая математику в 4 классе, ученики готовятся к более сложным темам, которые будут изучены в последующих классах. От правильного освоения основных понятий и навыков в четвертом классе зависит успех дальнейшего изучения математики.

Задача №5

Сколько квадратов изображено на рисунке.

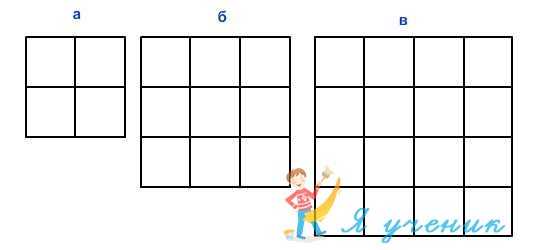 Подсчет ведем по количеству клеток-квадратиков в большем квадрате.

Начнем с варианта а.

В квадрате 4 клеточки, плюс сам квадрат

Итого 5 квадратов.

Вариант Б

Воспользуемся методом раскраски.

В квадрате 9 маленьких квадратиков, плюс сам квадрат, плюс 4 квадрата по 4 клетки.

 

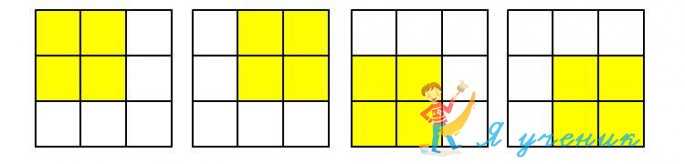
Итого 14 квадратов.

Вариант В

Одноклеточных квадратов — 16 (4 ряда по 4 клетки в ряд )

Четырехклеточных квадратов — 9 (3 по 3) 

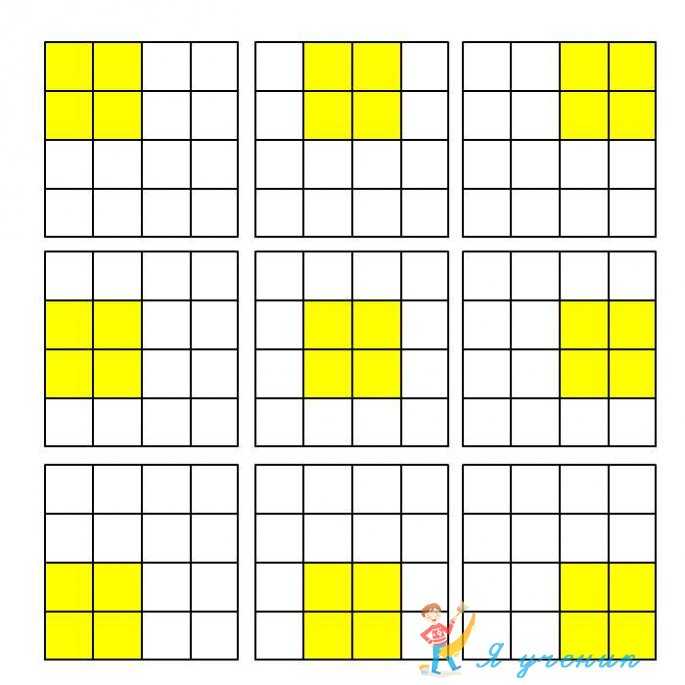 Трехклеточных квадратов 4 (2 по 2).

Четырехклеточный квадрат 1.

Итого.

16 + 9 + 4 + 1 = 30

Ответ: 30 квадратов.

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!

Задача №1.

Сколько треугольников изображено на рисунке.

 

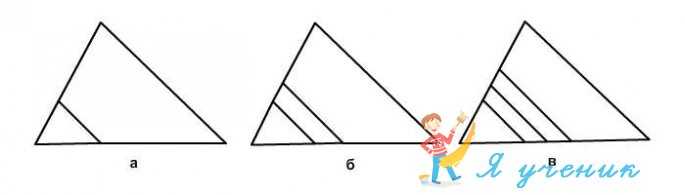
Есть три варианта рисунков — а, б, в.

Такого плана задания обычно не вызывают проблем, но все-таки разберем их, чтобы показать, как надо рассуждать при решении таких задач.

Рисунок А.

Обозначим уголки треугольника буквами A, B, C.

Проведем отрезок KL. Точка K лежит на на стороне треугольника AB, точка L лежит на стороне треугольника AC.

Был треугольник ABC. Добавился треугольник AKL.

Итого, получилось, что на рисунке всего 2 треугольника.

Рисунок Б.

 Обозначим уголки треугольника буквамиA, B, C.

Проведем отрезокKL. ТочкаKлежит на на стороне треугольникаAB, точкаLлежит на стороне треугольникаAC.

Проведем отрезокNM. ТочкаNлежит на на стороне треугольникаAB, точкаMлежит на стороне треугольникаAC.

Был треугольникABC. Добавился треугольникAKL.

Добавился треугольникANM.

Итого, получилось, что на рисунке всего 3 треугольника.

Советы по быстрому и точному решению задач с треугольниками

Прочитайте условие задачи внимательно

Важно понять, что от вас требуется и какие данные даны
Обратите внимание на то, какие свойства треугольников можно использовать для решения задачи.

Составьте план решения задачи. Прежде чем приступить к самому решению, определитесь с последовательностью шагов, которые вам нужно выполнить
Не торопитесь, на этом этапе можно потратить немного больше времени, но зато будете уверены в правильности решения.

Используйте свойства треугольников

Знание основных свойств треугольников поможет вам сэкономить время и решить задачу более точно. Используйте формулы для вычисления периметра, площади и других параметров треугольника. Также учтите особенности равносторонних, прямоугольных и других видов треугольников.

Разберите случаи и граничные условия. В некоторых задачах важно учесть особые случаи и граничные условия. Не забывайте о треугольниках, которые могут быть вырожденными, а также о случаях, когда предоставлены недостаточные данные для решения задачи.

Проверьте свое решение. Когда вы закончили решать задачу, не забудьте проверить свое решение. Пересчитайте все вычисления, проведите дополнительные проверки и удостоверьтесь, что ваш ответ правильный.

Применение этих советов поможет вам быстро и точно решать задачи с треугольниками и получать хорошие результаты на олимпиадах и экзаменах. Постоянная практика и знание основных свойств треугольников помогут вам стать настоящим экспертом в этой области.

Количество треугольников в зависимости от положения сторон

Для подсчета количества треугольников на каждом рисунке в 4 классе, необходимо учитывать положение сторон треугольника. Различные положения сторон могут привести к различным вариантам треугольников.

Существует три основных положения сторон треугольника:

1. Разносторонний треугольник — каждая сторона имеет уникальную длину. Количество разносторонних треугольников можно вычислить по формуле C(n, 3), где n — количество доступных сторон.
2. Равнобедренный треугольник — две стороны имеют одинаковую длину. Количество равнобедренных треугольников можно вычислить по формуле n * C(m, 2), где n — количество доступных сторон для равных сторон, m — количество допустимых равных сторон.
3. Равносторонний треугольник — все стороны имеют одинаковую длину. В этом случае, количество равносторонних треугольников равно количеству доступных сторон.

Для каждого рисунка в 4 классе, необходимо определить положение сторон треугольника и применить соответствующую формулу для подсчета количества треугольников. Затем, сложить результаты для каждого рисунка, чтобы получить общее количество треугольников.

Пример:

Рисунок	Положение сторон	Количество треугольников
Рисунок 1	Разносторонний	6
Рисунок 2	Равнобедренный	18
Рисунок 3	Равносторонний	3
Рисунок 4	Разносторонний	9

Всего треугольников: 6 + 18 + 3 + 9 = 36

Таким образом, общее количество треугольников на всех рисунках в 4 классе равно 36.

Понимание задачи и поиск треугольников

При анализе рисунка следует обратить внимание на наличие прямых отрезков, образующих треугольники. Необходимо исследовать каждый отрезок и определить, можно ли с ним образовать треугольник в сочетании с другими отрезками

Важно помнить, что каждый отрезок должен соединять три различные точки. При поиске треугольников на рисунке можно использовать тактику последовательного перебора всех возможных комбинаций отрезков

Для этого стоит внимательно просмотреть рисунок и записать все отрезки

При поиске треугольников на рисунке можно использовать тактику последовательного перебора всех возможных комбинаций отрезков. Для этого стоит внимательно просмотреть рисунок и записать все отрезки.

Затем можно создать список комбинаций отрезков, которые могут образовывать треугольники. Не забывайте о том, что треугольники могут быть разных видов (равносторонние, равнобедренные, прямоугольные и т. д.), поэтому стоит учесть все возможные варианты форм и размеров треугольников.

Последний шаг в решении задачи — подсчет количества треугольников. Для этого нужно проверить каждую комбинацию отрезков из списка на соответствие критериям треугольника и занести успешные комбинации в новый список. После этого просто посчитайте количество элементов в новом списке, чтобы получить ответ на вопрос задачи.

Использование рисунков в учебном процессе

Один из способов использования рисунков в учебном процессе – задачи, основанные на изображениях. Такие задачи требуют логического мышления, способствуют развитию наблюдательности и умения анализировать информацию.

Примером задачи, которая может быть построена на основе рисунка, является задача о количестве треугольников. В задаче ученик должен посчитать все треугольники на рисунке. Такая задача помогает развить навыки геометрического анализа, абстрактного мышления и счета.

Задачи, основанные на рисунках, также могут включать элементы других учебных предметов, например, учебу в русском языке или искусстве. Такие задачи помогают ученикам связывать различные области знаний и усиливают их понимание материала.

Использование рисунков в учебном процессе позволяет ученикам визуализировать и конкретизировать абстрактные понятия, что помогает им лучше понять и запомнить материал. Кроме того, рисунки способствуют активизации творческого мышления и развитию воображения.

В итоге, использование рисунков в учебном процессе является не только полезным и эффективным, но и интересным для учеников. Они не только улучшают понимание учебного материала, но и делают обучение более увлекательным и запоминающимся.

Методика подсчета числа треугольников без перебора

Для начала, следует обратить внимание на особенности треугольников. Треугольник образуется тремя линиями, которые встречаются в одной точке

Это означает, что для каждой точки на рисунке нужно посчитать, сколько треугольников можно образовать, если использовать эту точку в качестве вершины.

Рассмотрим пример. Дан рисунок, состоящий из 9 точек, расположенных в виде треугольника. Построим треугольники, используя каждую точку в качестве вершины:

Точка 1: соединяем точку 1 с любыми двумя другими точками — получаем 8 треугольников.

Точка 2: соединяем точку 2 с любыми двуми другими точками — получаем 8 треугольников.

Точка 3: соединяем точку 3 с любыми двуми другими точками — получаем 8 треугольников.

Точка 4: соединяем точку 4 с любыми двуми другими точками — получаем 8 треугольников.

Точка 5: соединяем точку 5 с любыми двуми другими точками — получаем 8 треугольников.

Точка 6: соединяем точку 6 с любыми двуми другими точками — получаем 8 треугольников.

Точка 7: соединяем точку 7 с любыми двуми другими точками — получаем 8 треугольников.

Точка 8: соединяем точку 8 с любыми двуми другими точками — получаем 8 треугольников.

Точка 9: соединяем точку 9 с любыми двуми другими точками — получаем 8 треугольников.

Суммируем эти значения и получаем общее число треугольников. В нашем примере это:

8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 72

Таким образом, общее число треугольников на данном рисунке составляет 72.

Такую методику можно применять и для более сложных рисунков, используя аналогичные шаги. Сначала находим число треугольников, образованных каждой вершиной, затем суммируем полученные значения.

Используя данную методику, можно эффективно решать задачи подсчета числа треугольников на рисунке без необходимости перебирать все возможные комбинации.