Урок математики на тему «слагаемое,слагаемое, сумма» презентация, доклад

Вычитание

Вычитание – это арифметическая операция, которая позволяет находить разницу между двумя числами.

Чтобы вычесть одно число из другого, необходимо изначально определить, какое число является уменьшаемым (то, из которого вычитают), а какое – вычитаемым (то, которое вычитают). Затем необходимо вычесть значение вычитаемого из уменьшаемого.

Пример: 7 – 3 = 4. Здесь число 7 является уменьшаемым, а число 3 – вычитаемым. Результат операции вычитания равен 4.

Если значение вычитаемого больше значения уменьшаемого, то результатом операции будет отрицательное число:

Пример: 3 – 7 = -4. Здесь число 3 является уменьшаемым, а число 7 – вычитаемым. Результат операции вычитания равен -4.

Можно также вычитать не только целые числа, но и дроби или десятичные дроби. В этом случае операция производится так же, как и в случае целых чисел.

Деление

Деление – это одна из арифметических операций, обратная умножению. Она позволяет находить один из множителей, если известен результат умножения и другой множитель.

Деление обозначается знаком «÷» или «/», а результат деления – знаком «=». Если результат деления содержит остаток, то его можно записать в виде дроби.

Пример деления: 12 ÷ 4 = 3. Здесь число 12 делим на число 4 и получаем результат – число 3, которое умноженное на 4 дает 12.

В математике существуют разные виды деления, например:

• Целочисленное деление – при котором остаток отбрасывается, результатом является целое число;
• Десятичное деление – при котором остаток учитывается, результат представляется десятичной дробью;
• Дробное деление – когда один множитель или результат являются дробями.

Важно помнить, что нельзя делить на ноль, так как это противоречит правилам математики и не имеет смысла

Считаем и решаем примеры до 20

Когда счет до 10 был освоен и ребенок стал свободно ориентироваться в первой десятке цифр, наступает время переходить на новый этап и обучаться двузначным числам, считать примеры в пределах 20.

Запоминаем цифры

Чтобы ребенок хорошо запоминал последовательность цифр, лучше всего использовать 20 одинаковых предметов (это даст возможность наглядно все объяснять малышу) или опять же карточки с числами.

Выглядеть это будет так:

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20

Поясняем ребенку, что в числах после 10 есть сходство. Визуализируя таким образом числа и десятки, вы поможете ребенку эффективнее запомнить их последовательность и названия. Видим число 11 – говорим «один» и прибавляем окончание «надцать». Так же поступаем и с другими двузначными числами – «три-надцать», «пять-надцать», «шесть-надцать» и т. д.

Работайте с ребенком на повторение, пока он не запомнит названия чисел.

Решаем примеры

Прежде чем приступить к решению примеров и обучению в пределах двадцати, дошкольник должен уяснить такие понятия, как «десятки» и «единицы». Для начального этапа обучения можно использовать кубики, палочки или попробовать учиться на счетах, а потом уже приучать малыша считать в уме. В возрасте 5 или 6 лет он должен уметь считать без помощи пальцев и других посторонних предметов.

Для первых занятий лучше использовать такие упражнения для детей, в которых не нужно совершать вычисления с переходом через десяток. Подойдут примеры, где все математические действия происходят с целым десятком или десятками и с некоторым количеством единиц, которые прибавляются либо вычитаются.

То есть десяток – основа всего примера.

Сложите кубики, палочки или другие предметы, с которыми вы работаете, по порядку в количестве 10 штук. Объясните малышу, что это десяток. Потом попросите прибавить к этому количеству еще несколько предметов, допустим 4. Говорите: «Десять плюс четыре равно четырнадцать». После того, как вы научили ребенка складывать, подобным образом составьте примеры с вычитанием, например:

18-8=10

13-10=3 и т. д.

Следующий этап – вычисления с переходом через десяток. Такие примеры даются ребятам несколько сложнее. Здесь уже понадобятся знания не только целых десятков и отдельных единиц, но и общее представление состава отдельного числа.

• Из чего состоит число 3? Из 1 и 2, или 1 и 1 и 1.
• А что такое 7? Это 1+6= 2+5= 1+1+1+4 и т. д.

Подобным образом поступите со всеми числами, которые знает ребенок, разберите их на составляющие части. Потом эти знания хорошо применить в решении примеров.

Разберем такой пример:

4+9=

Второе слагаемое раскладываем на два составляющих числа, чтобы при сложении с первым слагаемым получить десятку, а потом прибавляем остаток:

4+(6+3)= 10+3=13, т. е. 4+9= 13

Закрепим знания еще несколькими примерами:

5+7=

5+(5+2)= 10+2= 12

или

8+9=

8+(2+7)= 10+7= 17

Таким же образом можно решать примеры с вычитанием:

16-7=

16-(6-1)= 10-1= 9

или

13-8=

13-(3-5)= 10-5= 5

То есть для того чтобы сделать вычисление, раскладываем второе слагаемое таким образом, чтобы при вычитании из первого слагаемого получилась десятка, а потом вычитаем оставшееся число.

Также удобно показать малышу работу со сложением и вычитанием в столбик. В таких примерах нагляднее видно десятки и единицы, что с чем складывать или вычитать.

Напоследок несколько рекомендаций родителям.

• Во время занятий математикой проявите терпение к своему маленькому ученику и не раздражайтесь от его непонимания, а тем более не кричите.
• Не давите на ребенка и не заставляйте заниматься, если ему не хочется. Отпустите его, ведь он все равно не сконцентрируется. А в следующий раз придумайте, как его заинтересовать занятиями.
• Контролируйте время занятий, не держите малыша часами за решением примера. 10-20 минут должно длиться одно занятие. Дети быстро теряют концентрацию, и долговременные занятия нельзя назвать эффективными.
• На досуге между делом постоянно тренируйтесь с малышом. Когда режете торт, считайте, сколько кусков получилось, когда сервируете стол, посчитайте количество гостей и попросите принести нужное количество тарелок и т. д.

Главное одно – спокойная обстановка, терпение и родительская любовь однажды все равно дадут положительный результат. Не равняйтесь на других, а занимайтесь своим ребенком. Помните, что все дети разные и всем нужен индивидуальный подход.

Как находить слагаемые в задачах на деление?

Решая задачи на деление, необходимо определить количество и величину слагаемых, чтобы получить правильный ответ.

Прежде всего, нужно разложить делимое на слагаемые, например, если дано число 18, то его можно разложить на 9 + 9, 12 + 6 или 10 + 8. Затем выберите один из этих вариантов и выполните деление.

Для определения количества слагаемых можно использовать таблицу деления. Например, если нам нужно разделить число 24 на 3, то мы можем разложить его на 3 слагаемых по 8 каждое. Соответственно, в таблице деления мы находим, что деление 24 на 8 дает результат 3.

Если число не делится нацело, то можно использовать дробные слагаемые. Например, если нужно разделить число 12 на 4, то мы можем разложить его на два слагаемых: 3 и 3.2. В таблице деления мы находим, что 12/3 = 4, а 12/3.2 = 3.75.

Иногда, при решении задач на деление, может потребоваться использовать дополнительные математические операции, такие как умножение и вычитание, чтобы получить правильный ответ. Но всегда помните о необходимости разложить число на слагаемые и выбрать оптимальный вариант.

Вопрос-ответ:

Что такое слагаемые в математике?

Слагаемые — это числа или переменные, которые складываются вместе в процессе математических вычислений. Например, в выражении 5+3=8 числа 5 и 3 являются слагаемыми.

Какие существуют виды слагаемых в математике?

В математике существуют два вида слагаемых: положительные и отрицательные. Положительное слагаемое — это слагаемое со знаком «+», а отрицательное — со знаком «-«.

Как использовать определение слагаемых в математических задачах?

Определение слагаемых может использоваться в различных математических задачах, в том числе при работе с алгебраическими выражениями, разложении многочленов, при решении уравнений и т.д.

Как найти количество слагаемых в выражении?

Чтобы найти количество слагаемых в выражении, нужно посчитать количество чисел (или переменных), которые складываются в этом выражении.

Какое количество слагаемых можно складывать вместе?

В математике можно складывать любое количество слагаемых, но в практике обычно используют до 4-5 слагаемых, чтобы сделать вычисления более простыми и быстрыми.

Какие есть примеры слагаемых?

Примеры слагаемых: в выражении 2a + 3b = 5c слагаемыми являются числа 2 и 3, переменные a и b. В выражении 7x^2 — 2 х + 4 слагаемыми являются 7x^2, -2x и 4.

Что такое сумма слагаемых?

Сумма слагаемых — это результат складывания двух или нескольких слагаемых. Например, в выражении 2+3=5 сумма слагаемых 2 и 3 равна 5.

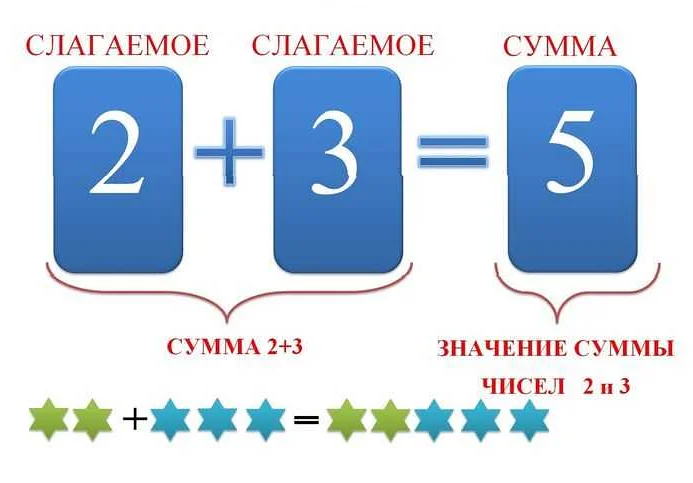
Класс 1: Сумма одинаковых положительных слагаемых

Класс 1 посвящен изучению суммы одинаковых положительных слагаемых. В этом классе дети учатся находить сумму нескольких одинаковых положительных чисел и изучают основные свойства этой операции.

Ученики начинают с простых примеров, где им предлагается найти сумму двух или трех одинаковых положительных чисел. Они учатся использовать сложение и применять его к повторяющимся числам.

Постепенно сложность примеров увеличивается, и ученикам предлагается находить сумму большего количества одинаковых положительных чисел. Они также изучают понятие «общая сумма» и учатся записывать ее в виде уравнения.

Один из важных аспектов, который изучается в этом классе, — это способность суммировать числа в разных порядках. Ученикам демонстрируются различные возможности упорядочивания слагаемых и рассказывается о том, что сумма будет одинаковой, независимо от порядка слагаемых.

В классе 1 также знакомят с упрощенными записями суммы и учатся использовать символы сложения и равенства для обозначения операции и результата.

Изучение суммы одинаковых положительных слагаемых в классе 1 позволяет детям развивать навыки сложения, понимание основных свойств сложения и способность работать с упрощенными записями математических операций.

Где используется сумма

В математике сумма является одной из основных арифметических операций. Она используется в различных математических дисциплинах, таких как алгебра, геометрия, теория вероятностей и т.д. Вот несколько примеров:

В арифметике сумма используется для нахождения общего количества при сложении двух или более чисел. В алгебре сумма используется для определения суммы значений переменных

Это важно при решении уравнений и систем уравнений. В геометрии сумма используется для нахождения площади фигур

Например, площадь прямоугольника равна сумме площадей его сторон. В теории вероятностей сумма используется для нахождения вероятности того, что событие произойдет как сумма значений двух или более случайных величин.

Кроме того, сумма используется в повседневной жизни. Например, когда мы складываем покупки в магазине, мы находим их сумму, чтобы узнать общую стоимость. Также сумма используется в финансовой сфере, при подсчете зарплаты, налогов и расходов компании.

Вопрос-ответ:

Как понять, что нужно сложить два числа?

В задании, как правило, указывается знак «+», который означает, что нужно складывать два числа. Также можно использовать слова «вместе» или «сумма».

Можно ли поменять порядок слагаемых при сложении?

Да, конечно! Порядок слагаемых можно менять, результат все равно будет одинаковым. Это свойство называется коммутативностью сложения.

Что такое ноль в сложении? Не меняет ли он результат?

Ноль в сложении называется нейтральным элементом. Если к числу прибавляется ноль, то результат не меняется, т.к. ноль никак не влияет на сумму.

Как найти сумму трех чисел?

Для сложения трех и более чисел нужно по очереди складывать все числа. Например, для сложения чисел 2, 5 и 8 нужно выполнить действие 2+5=7, а затем прибавить к этому результату число 8, получив сумму 15.

Можно ли сложить цифры в разных порядках, если их написали друг за другом?

Да, можно. Порядок цифр не влияет на сумму. Например, если написать цифры 2, 5 и 8 после друг друга, то получится число 258. Его можно разбить на слагаемые и выполнить сложение 2+5+8=15.

Сложение дробей

В математике мы изучаем, как складывать и вычитать числа, в том числе дроби. Для сложения дробей необходимо найти общий знаменатель, чтобы привести дроби к одинаковому виду, а затем сложить числители. Например, чтобы сложить дроби 1/4 и 3/8, необходимо найти общий знаменатель — в данном случае это 8.

Чтобы привести дробь 1/4 к знаменателю 8, нужно умножить ее на 2/2, а чтобы привести дробь 3/8 к знаменателю 8, нужно умножить ее на 1/1. Таким образом, получаем 2/8 и 3/8. Затем мы просто складываем числители 2 и 3, получаем 5, и записываем ответ 5/8.

Иногда может возникнуть ситуация, когда требуется сложить больше двух дробей. В таком случае необходимо сначала сложить две первые дроби, затем сложить полученную сумму с третьей дробью, затем сумму с четвертой дробью и т.д.

Проверка результата вычитания сложением

Проверка результата вычитания двух натуральных чисел базируется на связи между вычитанием и сложением. Там мы выяснили, что если c+b=a, то a−b=c и a−c=b. Если a−b=c, то c+b=a; если a−c=b, то b+c=a. Докажем справедливость данных равенств.

Пусть из a отложили в сторону b, после чего осталось c. Этому действию соответствует равенство a−b=c. Мы вернем отложенные b на место, то плучим a. Тогда можно говорить о справедливости равенства c+b=a.

Теперь мы можем сформулировать правило, позволяющее проверить результат вычитания сложением: нужно к полученной разности прибавить вычитаемое, при этом должно получиться число, равное уменьшаемому. Если полученное число не равно уменьшаемому, то при вычитании допущена ошибка.

Осталось лишь разобрать решения нескольких примеров, в которых выполняется проверка результата вычитания при помощи сложения.

Пример 24

Из 50 было вычтено 42 и было получено 6. Правильно ли было выполнено вычитание?

Проверим полученный результат вычитания. Для этого прибавим к полученной разности вычитаемое: 6+42=48 (если нужно, изучите другие параграфы по данной теме). Так как мы получили число, не равное уменьшаемому 50, то можно утверждать, что вычитание было проведено неправильно. Была допущена ошибка.

Пример 25

Необходимо определить разность 1 024−11 и проверить результат.

Вычисляем разность: 1 024−11=1 024−(1+10)=(1 024−1)−10=1 023−10=1 013.

Теперь выполняем проверку:

1 013+11=(1 000+10+3)+(10+1)==1 000+10+10+3+1=1 000+20+4=1 024

Получили число, равное уменьшаемому, следовательно, разность вычислена правильно. 1 024−11=1 023.

Действие вычитание. Знак-

Название компонентов действия вычитания

Давай продолжим раскрывать тайны науки математики

Ведь есть еще одно очень важное математическое действие, с которым нам обязательно нужно познакомиться

Итак, гномики закончили свою работу и возвращаются домой.

Дома их ждет Белоснежка. 

Она приготовила для гномиков угощение – испекла пирожные. Посчитай, сколько их получилось.

У тебя тоже получилось девять пирожных? Значит, ты посчитал правильно!

Когда гномики пришли домой, каждый из них съел по пирожному. Помнишь, сколько было гномов у Белоснежки? Точно, семь. Они съели столько же пирожных, т.е. тоже семь.

Давай зачеркнем съеденные пирожные.

Мы видим, что осталось совсем мало – всего два пирожных. Наверное, они достанутся Белоснежке.

В математике действие, которое ведет к уменьшению количества предметов, называется вычитание. Его смысл в следующем. Из целого множества удаляется его часть. В итоге остается меньше элементов, чем их было в целом множестве.

Чтобы узнать результат действия вычитания, нужно пересчитать элементы, которые остались.

Давай подумаем, в каких случаях предметов станет меньше. Пирожных стало меньше, потому что гномики съели часть из них. Еще могут быть такие ситуации:

• отдали;
• забрали;
• улетели (ушли, уехали);
• продали;
• использовали;
• сломали.

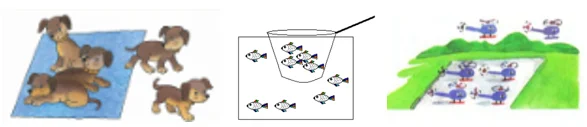
Для того, чтобы записать действие вычитания в виде математического выражения используют специальный знак. Знак вычитания выглядит так.

Он называется «минус».

В тетради знак «минус» пишется так.

Порядок написания знака «минус» следующий.

1. Ставим ручку чуть правее середины левой границы клетки.
2. Ведем горизонтальную прямую линию вправо.
3. Останавливаемся, немного не доходя до середины правой границы клетки.

Потренируйся писать знак «минус» в тетради.

А теперь я расскажу, как составлять математическое выражение, которое описывает действие вычитание.

Вспомни, сколько пирожных было сначала?

Правильно, 9. Запиши.

9

Гномики съели пирожные и их стало меньше, поэтому ставим знак «минус».

9 –

Они съели 7 пирожных. Запишем это число.

9 – 7

Ставим знак равенства и запишем количество пирожных, которые остались. Их оставалось 2.

9 – 7 = 2

В тетради запись выглядит так.

Названия компонентов действия вычитания запомнить довольно легко.

1. Первое число в результате вычитания станет меньше. Поэтому его называют уменьшаемое.
2. Второе число показывает, сколько надо вычесть. Значит оно вычитаемое.
3. В результате мы определяем какая разница между тем, что было и тем, что осталось. Поэтому результат действия вычитания называется разность.

Левая сторона этого выражения тоже называется разность.

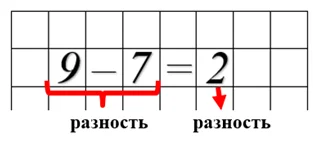
Если в задании говорится, что нужно «найти разность чисел», значит, следует составить математическое выражение с действием вычитания.

Такое выражение можно прочитать по-разному.

1. Из девяти вычесть семь будет два.
2. Девять минус семь получим два.
3. Уменьшаемое девять, вычитаемое семь, разность два.
4. Разность чисел девять и семь равна двум.

Закрепим все, что ты узнал о действии вычитания и составим математическое выражение по такой картинке.

Посмотри, сколько всего было шариков у гномика сначала? Запиши.

Правильно, пять.

Что случилось с некоторыми шариками? Сколько таких шаров?

Верно, два шарика сдулись и у гномика шариков осталось меньше. Значит нужно написать «минус два».

5 – 2

Ставим знак равенства и пересчитаем, сколько осталось целых шариков.

Их три.

5 – 2 = 3

Вот мы и составили выражение.

А теперь разберемся, как нужно решать примеры на вычитание. Например, посчитаем, сколько будет:

6 — 4

Назови уменьшаемое. Выложи столько же кружочков. Их должно быть 6.

Теперь назови вычитаемое. Убери (отодвинь, зачеркни) четыре кружочка.

Пересчитай кружочки, которые остались, и ты узнаешь ответ. Запиши его после знака равенства.

6 – 4 = 2

Мы решили пример на вычитание. Теперь ты знаешь, что обозначает это математическое действие, как называются компоненты вычитания, и как нужно составлять и решать математические выражения с действием вычитания.

Вычитание единиц из десятков, сотен, тысяч

Из числа 10 возможно любое число от 1 до 9. Воспользуемся представленной выше таблицей. Но что делать в других случаях? Необходимо представить приведенное как сумму двух слагаемых, одно из которых равно 10, а затем вычесть его из суммы. Закрепим наши знания материала на примере:

Пример 10

Вычтите 5 из 60.

Число 60 представляется в виде суммы двух чисел, одно из которых равно 10. Другое число находится путем вычитания числа 10 из 60. Так как 60−10=50, то 60=50+10. Заменим 60 на сумму 50+10 и получим 60−5=(50+10)−5. Получаем, что: (50+10)−5=50+(10−5)=50+5=55.

Рассмотрев вычитание единиц из десятков, перейдем к вычитанию единиц из сотен.

Чтобы вычесть из 100 число от 1 до 10, нужно представить 100 как 90 + 1090 + 10 и прибегнуть к правилу.

Пример 11

Необходимо найти разницу 100−7.

Представим 100 как 90+10 и выполним: 100−7=(90+10)−7=90+(10−7)=90+3=93. Усложним пример. Вычтем из числа 500 число 3. Представим 500 в виде суммы. Второй член = 500−100, то есть 400. У нас 500=400+100. 100=90+10, 500=400+90+10.

Таким образом, 500−3=(400+90+10)−3.

Завершим математику: (400+90+10)−3=400+90+(10−3)=400+90+7=497.

Перейдем к вычитанию единиц из тысяч.

Пример 12

Необходимо вычислить разницу 1000−8.

Так как 1000=900+100 и 100=90+10, то 1000=900+90+10.

Тогда 1000−8=(900+90+10)−8=900+90+(10−8)=900+90+2=992.

Пример 13

Из 7000 нужно вычесть единицу.

запишем 7000 как 7000=6000+1000=6000+900+100=6000+900+90+10.

Мы заключаем:
7000−1=(6000+900+90+10)−1=6000+900+90+(10−1)=6000+900+90+9=6999.

Используя этот пример, мы можем вычитать любое число, в том числе тысячные и десятитысячные.

Пример 14

Необходимо вычислить разницу 100 000−4.

Потому что
100 000=90 000+10 000=90 000+9 000+1 000==90 000+9 000+900+100=90 000+9 000+900+90+10
что
100 000−4 = (90 000 + 9 000 + 900 + 90 + 10) −4 = = 90 000 + 9 000 + 900 + 90 + (10 − 4) = 90 000 + 9 000 + 900 + 90 + 6 = 99 996.

Пример 15

Нужно от 4 000 000 отнять число 5.

Потому что
4 000 000 = 3 000 000,000+1 000 000 = 3 000 000+900 000+100 000 == 3 000 000+900 000+90 000+10 000 = 3 000 000+900 000+90 000+9 000+1000+1 000,00 000+90 000+900+900+100 == 3 000+900 000+90 000++90 000+900+100 == 3000+900 000+90 000,000+90 000+900+100 = 9000+900+90+10
что
4 000 000−5= (3 000 000+900 000+90 000+9 000+900+90+10) 5) ==3 000 000+900 000+90 000+9 000+9003+9,9.

Примеры и задачи

Пример 1 Расчет:

1) 15 – 5 – 3;

2) 16 — 6 — 1;

3) 18 – 8 – 9.

Решение:

1) 15 — 5 — 3 = 10 — 3 = 7;

2) 16 — 6 — 1 = 10 — 1 = 9;

3) 18 — 8 — 9 = 10 — 9 = 1.

Пример 2 Расчет:

1) 11-7;

2) 17-9;

3) 14 — 5.

Решение:

1) 11 — 7 = 11 — 1 — 6 = 10 — 6 = 4;

2) 17 — 9 = 17 — 7 — 2 = 10 — 2 = 8;

3) 14 — 5 = 14 — 4 — 1 = 10 — 1 = 9.

Упражнение 1. У Маши было 16 рублей. Она купила карандаш за 7 рублей и конфету за 8 рублей. Сколько денег осталось у Маши?

Решение:

16 — 7 = 9 — количество рублей, оставшееся после покупки карандаша;

9 — 8 = 1 — количество рублей, оставшееся после покупки конфеты.

Ответ: 1 рубль.

Задача 2. В одной коробке было 13 конфет, а в другой — 9 конфет меньшего размера. Сколько конфет было в двух коробках?

Решение: Сначала найдите, сколько конфет во второй коробке:

13 — 9 = 4.

Теперь найдем общее количество конфет, прибавив количество конфет в первой коробке к количеству конфет во второй коробке:

13 + 4 = 17.

Ответ: 17 конфет.

Приемы сложения и вычитания вида□ + 6, 7, 8, 9, □–6, 7, 8, 9

Поселились все зверюшки вместе в теремке. И дружно вместе принялись записывать остальные таблицы. Все примерах в них составляются на основе тех правил, о которых напомнила нам лисичка. Давай поможем им.

Начнем с таблицы сложения числа 6.

В предыдущих таблицах есть только четыре примера, в которых встречается слагаемое 6. Найди их.

Вот что выписали зверята.

Теперь переставляем слагаемые местами.

А теперь из этой таблицы мы легко можем составить таблицу вычитания числа 6. Попробуй сделать это самостоятельно.

Посмотри, какую таблицу вычитания числа 6 записали наши друзья.

Вот мы и закончили! У нас получилось составить таблицы сложения и вычитания числа 6.

Продолжаем. С таблицей сложения числа 7 нам повезло еще больше, ведь в ней будет всего три примера. Ты уже нашел их? Вот что записали зверята.

Надеюсь, ты не забыл еще переместительное свойство действия сложения, ведь оно нам пригодится при составлении таблицы с числом 7.

Подумай над этим сам. А потом проверь.

Все правильно. Теперь из предыдущей таблицы составим таблицу вычитания числа 7.

Не спеши, сделай это самостоятельно.

Проверь свою таблицу.

Как быстро ты со всем справился.

Дальше будет еще легче. Вспомни примеры, где встречается слагаемое 8.

В таблице сложения числа 8 всего два примера. Составь их.

Давай проверим.

Теперь составь таблицу вычитания числа 8.

Вот что получилось у наших друзей.

Вот мы и выучили таблицы сложения и вычитания с числом 8.

Ты, наверное, уже немного устал. Но нам осталось познакомиться всего с одной таблицей. Это таблица сложения и вычитания с числом 9.

Ты уже нашел пример с числом 9? Уверена, что ты справился. Назови его.

9 + 1 = 10

Давай переставлять. Что у нас получится?

1 + 9 = 10

Вот и вся таблица сложения с числом 9. Переходим к таблице вычитания числа 9.

У тебя уже все готово?

Правильно.

10 − 9 = 1

Мы с тобой неплохо потрудились и составили все таблицы в пределах 10. Вот как выглядит общая таблица сложения.

В этой таблице красным цветом выделены примеры, которые составлены путем перестановки слагаемых. Их запомнить очень легко.

А вот общая таблица вычитания чисел в пределах 10.

В этой общей таблице хорошо видны несколько закономерностей, которые помогут тебе лучше и быстрее запомнить результаты указанных математических выражений на вычитание.

1. В результате вычитания числа 1 получается число, которое является предыдущим по отношению к уменьшаемому.
2. В примерах, где уменьшаемое и вычитаемое являются «соседями» в натуральном ряду чисел, разность равна 1.
3. В таблице есть «парные» примеры, которые можно составить из одного и того же примера на сложение.

В этих выражениях компонентами являются одни и те же числа. Присмотрись и найди другие подобные пары примеров.

Чтобы получше запомнить все примеры из таблиц сложения и вычитания чисел в пределах 10, почаще тренируйся. Не забудь о наших сегодняшних помощниках.

Таблицы сложения и вычитания числа 1 мы выучили с помощью мышки, которая переходила маленькими шагами с числа на соседнее число. Как найти результаты в таблицах сложения и вычитания числа 2 нам подсказала лягушка, которая умеет прыгать через число. Зайчик показал, как узнать ответы в примерах из таблиц сложения и вычитания числа 3, который скачет так высоко, что может перепрыгнуть через два числа сразу. А двойной прыжок лягушки поможет вспомнить результаты таблиц сложения и вычитания числа 4. Лисичка же разгадала закономерности составления всех остальных таблиц.

Обязательно используй все приемы, которые нам подсказали герои нашей сказки. Чем чаще ты будешь повторять примеры из таблиц, тем быстрее ты запомнишь результаты каждого из них. Надеюсь, ты легко справишься с проверочными заданиями к этому уроку.

Общий приём сложения однозначных чисел с переходом через десяток

Итак, поговорим о сложении однозначных чисел. Ты уже знаешь, что обозначает это действие. Давай решим пример.

6 + 3 =

Посмотри, первое слагаемое в этом примере 6. Давай отсчитаем на счетах шесть косточек.

Второе слагаемое 3. Добавим три косточки.

Теперь пересчитаем все косточки вместе. Получим 9.

Значит, 6 + 3 = 9.

Это очень простой пример на сложение числа 6 с однозначными числами. Главная особенность таких примеров в том, что их результат не больше 10.

На счетах каждая палочка имеет по 10 косточек – ровно один десяток. Этого достаточно, чтобы решить любой пример на сложение в пределах 10.

Но сегодня мы будем учиться решать математические выражения другого вида. Сейчас мы разберем один пример и определим в чем заключается их особенность.

Как вычислить сумму

В математике сумма — это результат сложения нескольких чисел, которые обычно называются «слагаемыми». Для вычисления суммы нужно сложить все числа, которые указаны в задаче, и записать ответ.

Для того, чтобы научиться вычислять сумму, необходимо знать основные правила арифметики: сложение и вычитание. Если у тебя есть несколько чисел, чтобы найти их сумму нужно сложить их друг с другом. Например, для вычисления суммы 3, 5 и 7, нужно выполнить действие 3 + 5 + 7 = 15.

Список слагаемых иногда можно записать в ряд. Это удобно, когда чисел много и вычислять их по отдельности сложно. Ряд чисел записывается следующим образом: 1 + 2 + 3 + 4 + … + n. В таком случае нужно сложить все числа от 1 до n. Например, ряд чисел от 1 до 5 будет выглядеть так: 1 + 2 + 3 + 4 + 5 = 15.

Также, чтобы вычислить сумму, можно использовать таблицу умножения. Если у тебя есть два числа, то для сложения их нужно найти на пересечении соответствующих строк и столбцов в таблице произведения. Например, для того чтобы найти сумму 4 и 6, нужно найти значение на пересечении четвертой строки и шестого столбца таблицы умножения: 4 + 6 = 10.

В любом случае, чтобы найти сумму, нужно очень внимательно читать условие задачи, правильно записать числа и правильно выполнить математическое действие.