Как проявляется симметрия в живой природе

Примеры в природе

В жизни называется билатеральной, она встречается наиболее часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.

Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.

Значение лучевой симметрии в животном мире

Эта форма симметрии имеет огромное значение в животном мире. Она позволяет животным эффективно координировать движение и маневрировать в окружающей среде. Они могут быстро изменять свое положение, реагировать на опасность и добывать пищу, благодаря симметричному расположению своих органов и конечностей.

Благодаря лучевой симметрии животные могут развивать высокую маневренность и скорость передвижения. Например, рыбы с лучевой симметрией способны маневрировать в воде, изменяя угол наклона своих плавников. Это позволяет им двигаться быстро и точно управлять своим положением.

Кроме того, лучевая симметрия также упрощает жизнь внутренним органам животного. Органы занимают свои места на обеих половинах тела и эффективно выполняют свои функции. Это способствует более эффективной работе организма в целом.

В результате, лучевая симметрия играет значительную роль в эволюции и адаптации животных к окружающей среде. Она обеспечивает им преимущество в передвижении, поиске пищи и выживании. Благодаря этому, животные могут эффективно взаимодействовать со своим окружением и успешно приспосабливаться к различным условиям жизни.

Изучаем зеркальную симметрию

По своей природе, ребенок не может сразу изобразить две половинки одного целого одинаково. Рисунки маленьких детей почти всегда корявые и ассиметричные. Поэтому, когда мы изучаем зеркальную симметрию нужно объяснить ребенку, что половинки каждого из окружающих его предметов, как и собственное тело малыша, симметричны. Для подобного стартового этапа изучения симметрии подойдет упражнение с рисунком половины знакомого ребенку предмета красками впритык к сгибу альбомного листа и его перебивание на другую половину таким образом, чтоб получился целый предмет. Увидев результат полученной работы, объясните ребенку, что целый мячик, яблочко или что-либо изображенное, получилось из нарисованной половинки и есть отображение симметрии в предмете

Такие рисунки будут научным пособием для юного ученика о важности симметрии в окружающей его реальности

Слайд 6При зеркальной симметрии осей симметрии три, но симметричных сторон только

одна пара. Потому что две другие стороны — брюшная и

спинная — друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих.

Для насекомых, рыб, птиц, животных характерно несовместимое с поворотной симметрией различие между направлениями «вперед» и «назад». Придуманный в известной сказке о докторе Айболите фантастический Тянитолкай представляется совершенно невероятным существом, поскольку у него симметричны передняя и задняя половины. Направление движения является принципиально выделенным направлением, относительно которого нет симметрии у любого насекомого, любой рыбы или птицы, любого животного. В этом направлении животное устремляется за пищей, в этом же направлении оно спасается от преследователей.

Основные понятия симметрии и ее виды.

Понятие симметрии пр
оходит
через всю историю человечества. Оно
встречается уже у истоков человеческого
знания. Возникло оно в связи с изучением
живого ор­ганизма, а именно человека.
И употреблялось скульпторами ещё в 5
веке до н. э. Слово “симметрия” греческое,
оно означает “соразмерность,
пропорциональность, одинаковость в
расположении частей”. Его широко
используют все без исключения направления
современной науки. Об этой закономерности
задумывались многие ве­ликие люди.
Например, Л. Н. Толстой говорил: “Стоя
перед черной доской и рисуя на ней мелом
разные фигуры, я вдруг был поражен
мыслью: почему симметрия по­нятна
глазу? Что такое симметрия? Это врожденное
чувство, отвечал я сам себе. На чем же
оно основано?”. Действительно
симметричность приятна глазу. Кто не
любо­вался симметричностью творений
природы: листьями, цветами, птицами,
живот­ными; или творениями человека:
зданиями, техникой, – всем тем, что нас
с детства окружает, тем, что стремится
к красоте и гармонии. Герман Вейль
сказал: “Симмет­рия является той
идеей, посредством которой человек на
протяжении веков пытался постичь и
создать порядок, красоту и совершенство”.
Герман Вейль – это немецкий математик.
Его деятельность приходится на первую
половину ХХ века. Именно он сформулировал
определение симметрии, установил по
каким признакам усмотреть наличие или,
наоборот, отсутствие симметрии в том
или ином случае. Таким обра­зом,
математически строгое представление
сформировалось сравнительно недавно
– в начале ХХ века. Оно достаточно
сложное. Мы же обратимся и еще раз
вспомним те определения, которые даны
нам в учебнике.

Базовые элементы

В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.

Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.

Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.

Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.

Симметрия

С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.

Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.

Изображение правильных предметов: всего несколько шагов до законченного рисунка

Прежде чем приступить к рисованию симметричного предмета, нужно его выбрать. В нашем варианте это будет ваза, но даже если она никак не напоминает то, что решили изображать вы, не отчаивайтесь: все шаги абсолютно идентичны. Придерживайтесь последовательности и все получится:

1. У всех предметов правильной формы есть так называемая центральная ось, которую при симметричном рисовании обязательно стоит выделить. Для этого можно даже воспользоваться линейкой и провести по центру альбомного листа прямую линию.
2. Далее внимательно посмотрите на выбранный вами предмет и постарайтесь перенести его пропорции на лист бумаги. Сделать это несложно, если с обеих сторон проведенной заранее линии, наметить легкие штрихи, которые впоследствии станут очертаниями рисуемого предмета. В случае с вазой необходимо выделить горлышко, донышко и самую широкую часть корпуса.
3. Не забывайте о том, что симметричное рисование не терпит неточностей, поэтому если есть некоторые сомнения относительно намеченных штрихов, или вы не уверены в правильности собственного глазомера, перепроверьте отложенные расстояния при помощи линейки.
4. Последний шаг — соединение всех линий воедино.

Правила выполнения

Графические диктанты лучше использовать на математических уроках, например в 1 классе. Выполнение связано с системой координат, счетом, геометрическими фигурами. Методика проведения состоит из нескольких этапов:

1. Подготовьте для ученика лист бумаги в клеточку. У себя держите готовый вариант диктанта.
2. Поставьте точку на ученическом листке. Это будет начало отсчета. Или попросите дошкольника сделать это самостоятельно, объяснив, сколько места нужно отступить.
3. Нарисуйте на бумаге для ребенка, только начинающего обучение, стрелочки, которые указывают направления сторон. Так легче получить правильный результат. На последующих занятиях подсказки уже не понадобятся.
4. Объясните, что 1 шаг – это клетка. Если делаем 2 шага, линия проходит 2 клетки.
5. Учитель диктует условия работы поэтапно.

На готовом листе для педагога есть рисунок, координатная плоскость, состоящая из стрелок, цифр. Например, чтобы нарисовать елочку, проложите линию по горизонтали в 1 клеточку, по вертикали – 3 клеточки, наискосок – 3 клеточки и так далее. Чаще это просто стрелочки и цифры без слов.

Педагог проговаривает, какие линии, куда, на какое расстояние чертят дошкольники. Инструкции даются друг за другом, не торопясь.

6. После выполнения письменных заданий, получения результата сделайте выводы об уроке, стараниях дошкольников. Пожурите за невнимательность, если ребенок отвлекался по пустякам, или похвалите за достижения.

Польза математических диктантов

Графический диктант для дошкольников — полезная методика для диагностики уровня развития и занятий по подготовке к школе в детском саду, дома.

В ДОУ воспитатели чаще используют пособия авторов: Д.Б. Эльконина, О.А. Холодовой. К.В. Шевелев разработал целый курс поэтапных занятий с детьми 4–5 лет, 5–6 лет, а также первоклассниками. Специальные тетради развивают следующие навыки и умения у дошколят из подготовительной группы:

координация движений;
внимание;
память;
усидчивость;
воображение;
словарный запас;
мелкая моторика;
орфографическая зоркость.

Одновременно с физическими навыками ребенок повышает самооценку. Он осознает необходимость восприятия инструкции на слух. Делает работу четко и быстро, не отвлекаясь на птичку в окошке или смех соседа по парте.

Еще одной задачей графической математики является расширение кругозора. Подбирать картинки нужно по возрасту и уровню развития малышей, но это только на первых порах. Позже рисуйте изображения, которые незнакомы дошкольникам. После начертания такой арифметической задачи на листе бумаги расскажите историю о необычном животном, познакомьте с местом обитания, покажите фотографию.

Числовые задания под диктовку хорошо адаптируют детсадовцев к школе. Учат шестилеток самостоятельности, ориентированию в новом пространстве. Это поможет в освоении программы начальной школы, при знакомстве с новым коллективом, педагогом.

Умение держать карандаш, выполнять устные инструкции, расшифровывать текст, писать – отличная база для подготовки к первому классу. Можно попросить ребенка распечатывать листы, шаблоны, помочь в интерпретации инструкции. Это помогает познакомить будущего дошкольника с офисной техникой, воспитать уважение к старшим.

Симметрия человека

Человеческое тело характеризует билатеральная зеркальность, проявляющаяся повторением парных органов по разным сторонам фигуры. Однако такую симметрию нельзя именовать совершенной, поскольку отклонения показывают степень приспособленности человека к определенной сфере деятельности.

Физическая схожесть не свидетельство равноценности. Только некоторым людям удается одинаково сноровисто пользоваться обеими своими руками. Обычно у большинства одна из них ведущая. Хотя внешне каждый из нас симметричен. Принято считать зеркально смотрящиеся лица более симпатичными. Да и фигура выглядит привлекательнее, когда она пропорциональна по законам симметрии. А вот если это правило нарушено, тело выглядит иногда уродливо, да и такое состояние чревато заболеванием.

Однако стопроцентная симметрия смотрится слишком скучно. Поэтому незначительные отклонения придают нам индивидуальность, некоторую «изюминку». При общей картине зеркальности в мелочах мы специально акцентируем асимметрию — делая, например, асимметричную прическу. Некоторые пришивают на пиджак асимметричный кармашек, с одной стороны цепляют ордена.

Иногда люди стремятся как-то еще усилить отличие сторон тела. Когда-то среди мужчин было принято носить штаны с разноцветными половинками. Совсем недавно популярными признавались джинсы, имеющие цветные пятна, разрывы. Однако подобные увлечения недолговечны, поэтому только незначительные отклонения от естественной симметрии сохраняются в неизменности.

Нормам симметрии практически подвластно все в живой окружающей природе. Даже облака, хоть и с небольшим искажением, ей подчиняются. Проявляясь везде, зеркальность отражает фундаментальные характеристики материальных предметов. Поэтому на скрупулезное исследование этого явления с целью сопоставить полученные результаты и дотошно их проанализировать, направлены усилия многих ученых. Изучение феномена станет удобным способом познания основополагающих критериев существования самой материи. Похожесть частей — настоящее равенство. Когда она присутствует, значит всегда что-то непременно сохранится неизменным.

Примеры животных с лучевой симметрией

Гриб — многие грибы также обладают лучевой симметрией. Например, шляпка гриба имеет круглую или дисковидную форму, что является примером лучевой симметрии.

Краб — карапакс(часть панциря, который покрывает спину) рака обладает лучевой симметрией. Он имеет приблизительно круглую или шестиугольную форму со множеством лучей, которые расходятся от одной точки.

Медуза — многие виды медуз обладают лучевой симметрией. Они имеют куполообразное тело, которое имеет лучи, расходящиеся из центральной точки.

Комар — у комаров расширенная голова и длинное тело обладают лучевой симметрией. Длинные ноги расположены сбоку и создают симметричный вид.

Звезда — морская звезда, известная также как морская звезда, обладает лучевой симметрией. Ее тело состоит из диска с пятью лучами, которые отходят от центральной точки.

Корова — у коровы передние и задние ноги располагаются сбоку и создают внешний вид лучевой симметрии. Это симметричное размещение конечностей делает их примером животного с лучевой симметрией.

Еж — спинные иглы у ежа расположены лучами, скрещивающимися вокруг его тела. Этот уникальный дизайн является примером лучевой симметрии у ежей.

Морские звезды

Морские звезды обитают во всех океанах и морях, на всех глубинах. Они предпочитают мягкие и песчаные дна, где могут легко присосаться своими ножками. Морская звезда ведет в основном скрытный образ жизни, питаясь мелкими животными, такими как раки, моллюски и другие беспозвоночные. Она использует свои тонкие и гибкие лучи для обхвата и вытащивания еды в свою пасть, находящуюся на нижней стороне тела.

Морская звезда имеет несколько защитных механизмов: некоторые виды морских звезд обладают ядовитыми шипами, которые могут проникнуть в кожу хищника, другие виды морских звезд способны отбрасывать и восстанавливать отрывающиеся лучи, чтобы отвлечь хищника и спастись.

Одним из самых известных видов морских звезд является песочная звезда. Она имеет плоское тело и песчаный цвет, что помогает ей скрыться на дне моря. Еще одним примером морской звезды является голубая звезда, которая обладает ярким синим цветом и является эмблемой одного из популярных курортов.

Губки

Среди примеров губок можно назвать:

• Морж: этот мощный животный вид характеризуется массивным телом, усы, большими клыками и способностью плавать в холодных водах.
• Медуза: эти прозрачные морские создания имеют форму колокола и обладают столетиями неизменной структурой. Они полностью состоят из желеобразной субстанции.
• Рыба: многие виды рыб обладают лучевой симметрией тела. Примеры включают карпа, треску и полосатую рыбу.
• Краб: эти позвоночные имеют панцирь и десять ног. Их тела также обладают лучевой симметрией, где все части собраны вокруг центральной оси.

Губки — уникальные создания, которые, несмотря на свою простоту, играют важную роль в экосистемах океанов и морей. Они представляют собой интересный объект изучения для биологов и морских исследователей.

Медузы

Медузы имеют прозрачное гелевидное тело, похожее на гриб или зонтик, с длинными щупальцами, которые позволяют им плавать и поедать пищу. Они не имеют головы, глаз или ушей, но способны реагировать на свет и температуру.

Медузы не являются самостоятельными организмами, они проходят несколько стадий развития, начиная с полипа и заканчивая медузой. Их размножение может происходить половым путем или путем продолжения полипической стадии.

Медузы встречаются в океанах и морях по всему миру. Некоторые из наиболее известных видов медуз включают приморскую медузу комара, нордского медузика, лунную медузу, ауроральную медузу и португальскую медузу. Они могут различаться по размеру, форме и цвету.

Медузы уникальны и могут быть красивыми, но некоторые из них также могут быть опасными для человека. Касание некоторых видов медузы может вызвать ожоги или другие проблемы со здоровьем

Поэтому следует проявлять осторожность, находясь вблизи известных обитателей моря

Название	Описание
Гриб	медузы имеют форму, похожую на гриб или зонтик
Комар	некоторые виды медузы имеют щупальца, похожие на ножки комара
Корова	медузы не имеют ног, их тело свободно плавает в воде
Морж	медузы могут иметь длинные щупальца, как у моржа
Краб	некоторые медузы могут иметь щупальца, напоминающие клешни краба
Рыба	медузы могут поедать рыбу в качестве пищи
Звезда	медузы могут иметь форму, напоминающую морскую звезду

Оно имеет одну поворотную ось 4-го порядка (ось АВ), четыре поворотные оси 2-го порядка (оси СЕ, DF , MP , NQ ), пять плоскостей симметрии (плоскости CDEF , AFBD , ACBE , AMBP , ANBQ ).

5

.

Переносная симметрия

Ещё одним видом симметрии является
переносная


с

имметрия.

О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние «а» либо расстояние, кратное этой величине, она совмещается сама с собой

Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние «а» — элементарным переносом, периодом или шагом симметрии.

а

Периодически повторяющийся рисунок на длинной ленте называется бордюром. На практике бордюры встречаются в различных видах (настенная роспись, чугунное литье, гипсовые барельефы или керамика). Бордюры применяют маляры и художники при оформлении комнаты. Для выполнения этих орнаментов изготавливают трафарет. Передвигаем трафарет, переворачивая или не переворачивая его, обводим контур, повторяя рисунок, и получается орнамент (наглядная демонстрация).

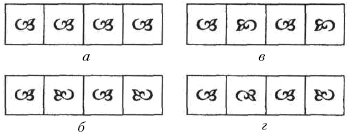
Бордюр легко построить с помощью трафарета (исходного элемента), сдвигая или переворачивая его и повторяя рисунок. На рисунке изображены трафареты пяти видов:
а

) несимметричный;
б, в

) имеющие одну ось симметрии: горизонтальную или вертикальную;
г

)

центрально-симметричный;
д

) имеющий две оси симметрии: вертикальную и горизонтальную.

Для построения бордюров используют следующие преобразования:

а

) параллельный перенос;
б

) симметрию относительно вертикальной оси;
в

) центральную симметрию;
г

) симметрию относительно горизонтальной оси.

Аналогично можно построить розетки. Для этого круг делят на
n

равных секторов, в одном из них выполняют образец рисунка и затем последовательно повторяют последний в остальных частях круга, поворачивая рисунок каждый раз на угол 360°/
n

.

Наглядным примером применения осевой и переносной симметрии может служить забор, изображённый на фотографии.

Вывод: Таким образом, существуют различные виды симметрии, симметричные точки в каждом из этих видов симметрии строятся по определённым законам. В жизни мы повсюду встречаемся тем или иным видом симметрии, а часто у предметов, которые нас окружают, можно отметить сразу несколько видов симметрии. Это создаёт порядок, красоту и совершенство в окружающем нас мире.

ЛИТЕРАТУРА:

Справочник по элементарной математике. М.Я. Выгодский. – Издательство « Наука». – Москва 1971г. – 416стр.

Современный словарь иностранных слов. — М.: Русский язык, 1993г
.

История математики в школе
IX

—

X

классы. Г.И. Глейзер. – Издательство «Просвещение». – Москва 1983г. – 351стр.

Наглядная геометрия 5 – 6 классы. И.Ф. Шарыгин, Л.Н. Ерганжиева. – Издательство «Дрофа», Москва 2005г. – 189стр.

Энциклопедия для детей. Биология. С. Исмаилова. – Издательство «Аванта+». – Москва 1997г. – 704стр.

Урманцев Ю.А. Симметрия природы и природа симметрии — М.: Мысль
arxitekt

arhkomp

2.

htm

,

, ru.wikipedia.org/wiki/

Сегодня мы с вами поговорим о явлении, с которым каждому из нас приходится постоянно встречаемся в жизни: о симметрии. Что такое симметрия?

Приблизительно мы все понимаем значение этого термина. Словарь гласит: симметрия – это соразмерность и полное соответствие расположения частей чего-нибудь относительно прямой или точки. Симметрия бывает двух видов: осевая и лучевая. Сначала рассмотрим осевую. Это, скажем так,«зеркальная» симметрия, когда одна половина предмета полностью тождественна второй, но повторяет ее как отражение. Поглядите на половинки листа. Они зеркально симметричны. Симметричны и половины человеческого тела (анфас) – одинаковые руки и ноги, одинаковые глаза. Но не станем заблуждаться, на самом деле в органическом (живом) мире абсолютной симметрии не встретить! Половинки листа копируют друг друга далеко не в совершенстве, то же относится к человеческому телу (присмотритесь сами); так же обстоит дело и с другими организмами! Кстати, стоит добавить, что любое симметричное тело симметрично относительно зрителя только в одном положении. Стоит, скажем, повернуть лист, или поднять одну руку и что же? – сами видите.

Подлинной симметрии люди добиваются в произведениях своего труда (вещах) — одежде, машинах… В природе же она свойственна неорганическим образованиям, например, кристаллам.

Но перейдем к практике. Начинать со сложных объектов вроде людей и животных не стоит, попробуем в качестве первого упражнения на новом поприще дорисовать зеркальную половинку листа.

Растения

Лучевая симметрия тела встречается не только у животных, но и у некоторых видов растений. Одним из примеров таких растений являются морские звезды. Они имеют форму пентагона и разделяются на пять одинаковых лучей. Также лучевая симметрия характерна для серпикообразных растений, у которых стебли и листья расположены вокруг центральной оси.

Еще одним примером растений с лучевой симметрией являются звенообразные растения. Их листья и цветки располагаются по кругу и создают эффект радиальной симметрии. Коралловые ползунки также обладают лучевой симметрией тела, их кораллиты имеют форму первоначального круга, который постепенно разделяется на отдельные лучи.

Головоусые растения также могут иметь лучевую симметрию. У них различные части растения, такие как цветки, листья или корни, расположены равномерно вокруг центральной оси. Кроме того, лучевая симметрия может быть характерна для некоторых видов губок. Они могут иметь форму круга или овала, а их поры располагаются по периферии симметрично подобно лучам.

В заключение, можно отметить, что лучевая симметрия тела встречается у различных видов растений, начиная от морских звезд до губок. Эта симметрия может проявляться в расположении листьев, цветков, корней и других частей растения вокруг центральной оси или в виде радиально расположенных лучей. Все эти примеры демонстрируют разнообразие и красоту ограниченной краской природы.

Цветы

Цветы — это разнообразные растения, которые привлекают внимание своей ограниченной краской и приятным ароматом. Они являются одним из наиболее популярных объектов природы для созерцания и украшения окружающей среды

Цветы обладают невероятной разнообразностью форм и цветов, благодаря которым они способны привлекать насекомых, таких как пчелы и бабочки, для опыления и размножения.

Многие виды цветов имеют лучевую симметрию тела. Они состоят из звеньев, которые равномерно расположены вокруг центральной оси. Этот тип симметрии можно наблюдать у таких цветов, как герань, сон-трава, подсолнух и роза. Они имеют вращательную симметрию, что делает их еще более привлекательными в глазах людей.

Помимо цветов, есть и другие живые организмы, которые также имеют лучевую симметрию тела. Например, морские звезды и головоусые обладают такой же симметрией, как и цветы. Их тело состоит из пяти или большего числа лучей, которые исходят из центральной точки. Эта симметрия делает их устойчивыми и гибкими в движениях, помогает им захватывать пищу и защищаться от хищников.

Еще один пример организмов с лучевой симметрией — коралловые ползуны. Они имеют особый вид симметрии, который называется серпикообразным. Их тело состоит из множества изломанных разветвленных частей, равномерно расположенных вокруг центральной оси. Эта симметрия делает их очень гибкими и позволяет им легко двигаться в морской среде.

И наконец, губки — еще одни животные с лучевой симметрией тела. Они имеют многочисленные отверстия и просветы, которые равномерно распределяются по всей их поверхности. Эта симметрия помогает им фильтровать пищу и защищаться от вредных веществ в воде. Губки являются одними из наиболее древних организмов на Земле и представляют собой уникальное разветвленное семейство живых существ.

Кувшинки

Кувшинки – это маленькие морские животные, которые принадлежат к группе головоусых или тикаловых. Они отличаются необычной формой тела, напоминающей кувшин. Тело кувшинки состоит из изломанных равномерным отростков, которые покрыты ограниченной краской, благодаря чему получается красивый узор.

У кувшинок коралловые ползунки покрывают внешнюю сторону их тела. Эти ползунки помогают им скользить и плавать в воде. Кувшинки живут на морском дне, где они питаются планктоном и другими мелкими организмами.

Кувшинки являются хищниками и используют свои губки, чтобы захватывать пищу. Когда кувшинка находит добычу, она опускает губки и быстро затягивает ее в свое тело. Затем она переваривает пищу и выбрасывает несъедобные остатки.

Некоторые виды кувшинок, такие как серпикообразные и морские звезды, могут размножаться путем отрывания части своего тела и образования нового организма. Этот процесс называется асексуальным размножением и позволяет кувшинкам быстро размножаться и распространяться по морскому дну.

Симметрия

«Симметрия в природе» — В 19 веке, в Европе, появились единичные работы, посвящённые симметрии растений. . Осевая Центральная. Одним из основных свойств геометрических фигур является симметрия. Работу выполнили: Жаворонкова Таня Николаева Лера Руководитель: Артёменко Светлана Юрьевна. Под симметрией в широком смысле понимают всякую правильность во внутреннем строении тела или фигуры.

«Симметрия в искусстве» — II.1. Пропорция в архитектуре. Каждый конец пятиугольной звезды представляет собой золотой треугольник. II. Центрально-осевая симметрия присутствует чуть ли не в каждом архитектурном объекте. Площадь Вогезов в Париже. Периодичность в искусстве. Содержание. Сикстинская мадонна. Красота многогранна и многолика.

«Точка симметрии» — Кристаллы каменной соли, кварца, арагонита. Симметрия в животном мире. Примеры вышеупомянутых видов симметрии. B А О Любая точка прямой является центром симметрии. Такая фигура обладает центральной симметрией. Круглый конус обладает осевой симметрией; ось симметрии – ось конуса. Равнобочная трапеция имеет только осевую симметрию.

«Движение в геометрии» — Движение в геометрии. Как движение используется в различных сферах деятельности человека? Что называется движением? К каких науках применяется движение? Группа теоретиков. Математика красива и гармонична! Можем ли мы видеть движение в природе? Понятие движения Осевая симметрия Центральная симметрия.

«Математическая симметрия» — Симметрия. Симметрия в математике. Типы симметрии. В х и м и и. Вращательная. Математическая симметрия. Центральная симметрия. Вращательная симметрия. Физическая симметрия. Тайна зеркального мира. Однако у сложных молекул, как правило, отсутствует симметрия. ИМЕЕТ МНОГО ОБЩЕГО С ПОСТУПАТЕЛЬНОЙ СИММЕТРИЕЙ В МАТЕМАТИКЕ.

«Симметрия вокруг нас» — Центральная. Один вид симметрии. Осевая. В геометрии есть фигуры, которые имеют. Вращения. Вращения (поворотная). Симметрия на плоскости. Горизонтальная. Осевая симметрия относительно прямой. Греческое слово симметрия означает «пропорциональность», «гармония». Два вида симметрии. Центральная относительно точки.

Всего в теме
32 презентации

Слайд 15У животных появление билатеральной симметрии в эволюции связано с ползанием по

субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животнымУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожихУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблийУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносомУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносом, бодонид, раковинок многих фораминиферУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листьяУ животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными