Какие бывают ломаные 2 класс математика

Публикация «Урок по математике в 1 классе „Ломаная линия“» размещена в разделах

• Математика, 1 класс
• Математика. Конспекты уроков
• Начальная школа. 1 класс
• Начальная школа. 1-4 классы
• Точка и линии
• Школа. Материалы для школьных педагогов
• Темочки

Метапредметные: понимать и принимать учебную задачу, осуществлять решение учебной задачи; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в изменённых условиях; слушать собеседника и вести диалог.

Личностные: проявлять интерес к математике, осваивать роль ученика на основе выполнения правил поведения на уроке; работать в паре и оценивать товарища.

Тип урока : изучение нового материала.

Технологии: ИКТ технология, игровая, личностно-ориентированная, групповая, здоровьесберегающая.

Оборудование: электронное приложение к учебнику М. И. Моро математика 1 класс, интерактивная доска, проектор, ноутбук, герой – Незнайка, кусок проволоки.

Слайды и текст этой презентации

Слайд 1I Международный конкурс
«Радуга презентаций – 2014» Ковальчук Ирина АлексеевнаМБОУ

образования

Ломаная

равны 5 см и 1 см соответственно.АВСАС = АВ +

ВС = 1 + 5 = 6 см

равны 2 см и 10 см соответственно.АВСАС = АВ +

ВС = 2 + 10 = 12 см

АВ = 17 – 3 = 14 см

ВС = 11 – 8 = 3см

равны 1 см и 100 см соответственно.АВСАС = АВ +

ВС = 1 + 100 = 101см

= 100 – 1 = 99см

1 см.MNKMN = NK = 1 см

см

длина отрезка MK?MNKMK = MN + NK = 1 +

1 = 2 см

= 5 см

= 100 см.MNKMK = MN +NK = 100 + 100

= 200 см

Слайд 19 Ломаная – это последовательное соединение нескольких отрезков, отрезки являются звеньями

– Звенья – Ломаная – А, В, САВ, ВС АВС,

СВА

А, В, С

АВ, ВС, АС

АВС, СВА, АСВ

= АВ + ВС АВС = АВ + ВС +

СА

Слайд 26 Отметьте в тетради точки A, B, C

и D, так же как на рисунке 18. Постройте какую

– нибудь другую незамкнутую ломаную, для которой эти точки тоже были бы вершинами. Запишите ее название.

Задание № 103

ACBD

А

С

В

D

Слайд 27 Сколько всего различных незамкнутых ломаных можно построить

с вершинами в точках А, B, C, D (рис. 18)

?

Задание № 104

А

С

В

D

А

С

В

D

А

В

С

D

А

С

В

D

А

С

В

D

А

С

В

D

Слайд 29 Постарайтесь объяснить, что такое длина ломаной.Начертите ломаную,

состоящую из четырех звеньев, измерьте их длины и запишите выражение,

соответствующее длине ломаной. Найдите значения выражения.

Задание № 106

M

K

E

N

P

Длина ломаной равна сумме всех звеньев, из которых она состоит.

MNKEP – незамкнутая ломанаяMNKEP = MN + NK + KE + EP = = 2 + 3 + 1 + 4 = 10 см

Слайд 302) Найдите длину ломаной, изображенной на рисунке 18.Задание № 106

ABCD– незамкнутая ломанаяABCD = AB + BC +

CD = 1 см 8 мм + 2 см 5 мм + + 1 см 9 мм = 6 см 2 мм

Слайд 312) Найдите длину ломаной, изображенной на рисунке 18.Задание № 106

ABCD– незамкнутая ломанаяABCD = AB + BC +

CD = 1 см 8 мм + 2 см 5 мм + + 1 см 9 мм = 6 см 2 мм

20

: 10

Не измениться

: 10

: 10

: 100

: 100

: 10

: 100

Слайд 33Найдите неизвестное число.Задание № 111а) 17 + ? = 100100

– 17 = 83б) 64 + ? = 100100 –

64 = 36

в) 24 + ? = 50

50 – 24 = 26

г) 36 + ? = 50

50 – 36 = 14

д) 6 + ? = 100

100 – 6 = 94

е) 73 + ? = 100

100 – 73 = 27

Слайд 34 Назвать ломаные, предложенные на рисунке, их вершины

и звенья. Найти длины ломаных.СВDА ABCD = AB + BC

+ CD = 2 + 3 + 2 = 7 см

2 см

3 см

2 см

Вершины –

А, В, С, D

Звенья –

АB, ВC, СD

Ломаная –

АBСD

Слайд 35 Назвать ломаные, предложенные на рисунке, их вершины

и звенья. Найти длины ломаных.SFTK KTSF = KT + TS

+ SF = 5 + 3 + 1 = 9 см

5 см

1 см

3 см

Вершины –

K, F, S, T

Звенья –

KT, TS, SF

Ломаная –

KTSF

Слайд 36Прочитать материал параграфа (стр. 33 – 34), выучить записанные

правила, выполнить задания № 105, 107, 114. Домашнее задание

в Adobe Photoshop CS3)2. Математика. 5 класс: поурочные планы по

учебнику И. И. Зубаревой, А. Г. Мордковича. – 2-е изд., стереотип./ авт. – сост. Е.А.Ким. – Волгоград: Учитель, 2008. – 285 с.3. Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений/ И. И. Зубарева, А. Г. Мордкович. – 9-е изд., стер. – М.:Мнемозина, 2009. – 270 с.: ил.

Признак замкнутости ломаной линии

Классификация ломаных линий прежде всего осуществляется по свойству замыкания.

Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.

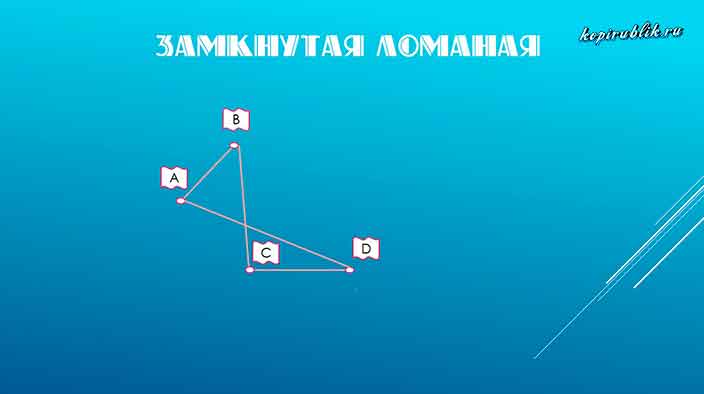
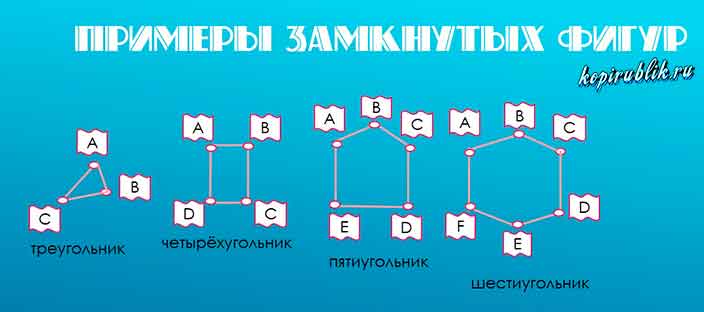
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:

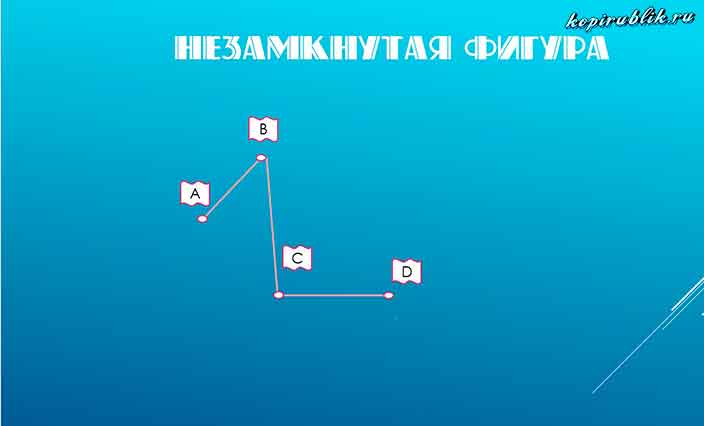
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.

Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».

В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.

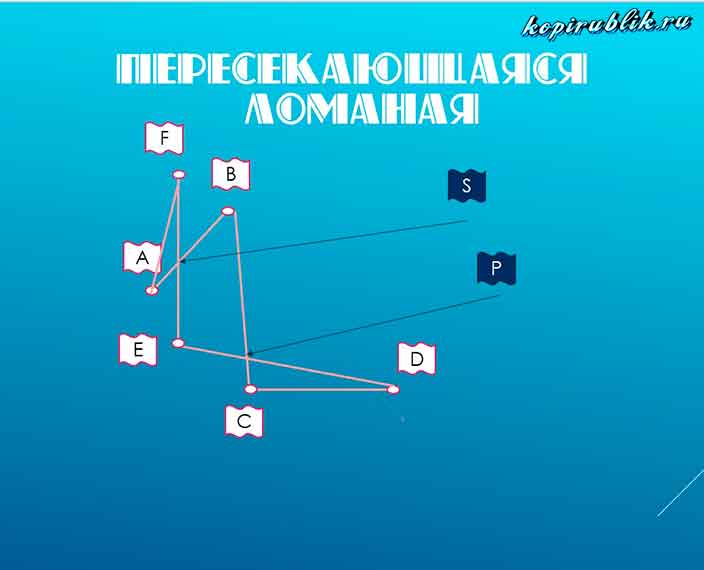
На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.

Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?»

Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:

Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.

Как создать ломаную: идеальный план для начинающих художников

Шаг 1: Подготовка материалов

Перед тем, как приступить к созданию ломаной, вам потребуются следующие материалы:

• Лист бумаги или холст
• Карандаш или маркер
• Линейка

Шаг 2: Определение вершин ломаной

Прежде всего, решите, сколько вершин вы хотите добавить в свою ломаную. В нашем случае, мы будем создавать ломаную с 3 вершинами. Найдите на вашем листе бумаги или холсте три точки, которые будут служить вершинами вашей ломаной.

Шаг 3: Рисование звеньев

Возьмите карандаш или маркер и начните рисовать от каждой вершины до следующей. Используйте линейку, чтобы сделать прямые линии или нарисуйте линии вручную, если хотите, чтобы они выглядели более природно. Подберите углы между звеньями в зависимости от того, какой вид эффекта вы хотите достичь. Ломаная может быть как острыми углами, так и сглаженными переходами — это зависит от вашего выбора.

Шаг 4: Окончание ломаной

Когда вы нарисовали звенья между всеми вершинами, закончите ломаную соединением последней вершины с первой. Убедитесь, что звено примыкает к первой вершине с четким углом или плавным переходом, чтобы создать законченный вид ломаной.

Шаг 5: Завершение работы

После того, как вы закончили рисование ломаной, пройдитесь по ней и убедитесь, что линии ровные и вершины соединены правильно. Если вы захотите, вы можете перерисовать линии более темным карандашом или маркером, чтобы ломаная выглядела более выразительно. Также не забудьте подписать вашу работу или добавить какие-либо дополнительные детали, если хотите.

Теперь, когда вы знаете, как создать ломаную, вы можете приступить к рисованию с уверенностью. Практикуйтесь, экспериментируйте с разными вариантами углов и внешним видом ломаной. Постепенно вы сможете преодолеть любые трудности и создать впечатляющие произведения искусства!

Работа с координатами

Для работы с координатами в HTML-формате используются различные атрибуты и свойства элементов. Например, для создания точки на плоскости можно использовать элемент с заданными значениями атрибутов и :

• Атрибут — задает горизонтальную координату точки (x)
• Атрибут — задает вертикальную координату точки (y)

Например:

Этот код создаст точку на плоскости с координатами (50, 100).

При соединении точек и создании ломаной необходимо учитывать порядок точек. Для этого можно использовать массив координат точек и пробежаться по нему, соединяя точки с помощью линий. Например, можно использовать тег и методы JavaScript для рисования линий между точками.

Важно помнить, что координаты могут быть положительными или отрицательными, и могут быть числами с плавающей запятой. Также стоит учесть, что координаты могут быть относительными, если используется относительное позиционирование элементов

Примеры построения ломаной на чертеже 1 класса страница 43

Ниже приведены примеры построения ломаной на чертеже для учащихся 1 класса по странице 43. Ломаная южна серия сплошных отрезков линий, которые соединены подряд так, что получившаяся линия имеет несколько углов.

Пример 1:

• Начните с точки A на чертеже.
• Проведите прямую линию до точки B.
• От точки B проведите еще одну прямую линию до точки C.
• Продолжайте проводить прямые линии поочередно до точек D, E и F.

Пример 2:

1. Начните с точки P на чертеже.
2. Проведите прямую линию до точки Q.
3. От точки Q проведите еще одну прямую линию до точки R.
4. Затем проведите линию до точек S и T.
5. Закончите ломаную в точке U.

Пример 3:

• Начните с точки X на чертеже.
• Проведите прямую линию до точки Y.
• От точки Y проведите еще одну прямую линию до точки Z.
• Продолжайте проводить прямые линии до точки W и V.
• Закончите ломаную в точке U.

Следуйте инструкциям и используйте примеры, чтобы научить учащихся построить ломаную на чертеже. Задачи с ломаными помогут детям развить навыки работы с графиками и координатной плоскостью.

Зачем рисовать ломаную?

Рисование ломаных потребует от ребенка:

• Понимания последовательности и связи между отрезками и углами;
• Умения соблюдать пропорции и масштабировать фигуры;
• Умения использовать линейку и карандаш для создания ровных и четких линий.

Рисование ломаных развивает важные навыки и наблюдательность:

• Логическое мышление – дети могут представить и нарисовать последовательность действий, чтобы получить нужную форму ломаной;
• Воображение – создание и модификация геометрических фигур требует креативного подхода и воображения;
• Мелкую моторику руки – рисование линий и углов помогает развивать мелкую моторику руки и координацию движений.

Рисуя ломаную линию, ребенок не только изучает геометрические формы и понятия, но и развивает важные навыки, которые понадобятся ему в будущем. Поэтому рисование ломаных является интересным и полезным занятием для первоклассников.

Правила отображения ломаной на чертеже

1. Все отрезки ломаной должны быть проведены на чертеже четкими и тонкими линиями. Ломаная может быть как закрытой, так и открытой.

2. Длина отрезков ломаной должна быть пропорциональна их значению и должна соответствовать заданным координатам на плоскости.

3. Ломаная должна быть отображена на чертеже таким образом, чтобы изображение было кратчайшим путем, соединяющим заданные точки.

4. Ломаная может быть изображена горизонтально, вертикально или под углом. В случае, если отрезки ломаной пересекаются, они должны быть правильно обозначены на чертеже.

5. Если на чертеже присутствуют несколько ломаных, каждая из них должна быть обозначена своим уникальным признаком, например, цветом или штриховкой.

Пример правильного отображения ломаной на чертеже:

Точка A	Точка B	Точка C	Точка D
Координаты: (1, 2)	Координаты: (3, 4)	Координаты: (5, 6)	Координаты: (7,
Ломаная
_________ / \ / \ /__ __\ A B C D

Правильное отображение ломаной на чертеже позволяет визуализировать последовательность точек и их связи, что очень важно при решении геометрических задач и построении графиков

Шаг 2: Рисование первого звена

Теперь, когда мы научились рисовать точки на бумаге с помощью карандаша, давайте начнем создавать нашу ломаную. Начнем с первого звена.

1. Возьмите лист бумаги и разместите его горизонтально перед собой.

2. Возьмите свой карандаш и на одном конце листа нарисуйте небольшой кружок. Это будет наше первое звено.

3. Запомните, что кружок — это специальная фигура, у которой все точки находятся на одинаковом расстоянии от центра. Постарайтесь нарисовать кружок как можно более точно.

4. Чтобы придать круглую форму кружку, приложите часть своей руки к листу и сделайте небольшое вращение кисти, продвигая карандаш по окружности.

Совет: Если у вас не получается нарисовать кружок с первого раза, не беда! Попробуйте еще раз

Важно помнить, что заниматься рисованием нужно с удовольствием и не бояться ошибаться

Теперь у вас есть первое звено вашей ломаной! Переходите к следующему шагу, чтобы нарисовать остальные звенья и завершить рисунок.

Изменение звена ломаной

Звено ломаной — это отрезок прямой, соединяющий две соседние вершины ломаной.

Изменение звена ломаной заключается в изменении длины или направления отрезка, соединяющего соседние вершины.

Если мы увеличиваем длину звена ломаной, то она становится более выпуклой. Если мы уменьшаем длину звена ломаной, то она становится более вогнутой.

Также можно изменять направление звена ломаной, поворачивая его в разные стороны. Например, если мы повернем звено ломаной влево, она будет иметь большую выпуклость влево.

Примеры изменения звена ломаной:

1. Увеличение длины звена ломаной:

• Изначальная ломаная: AB — BC — CD
• Изменение звена BC: AB — B1C1 — CD
• Ломаная после изменения: AB — B1C1 — CD

Уменьшение длины звена ломаной:

• Изначальная ломаная: AB — BC — CD
• Изменение звена BC: AB — B2C2 — CD
• Ломаная после изменения: AB — B2C2 — CD

Изменение направления звена ломаной:

• Изначальная ломаная: AB — BC — CD
• Изменение звена BC: AB — BC1 — CD
• Ломаная после изменения: AB — BC1 — CD

Важно понимать, что изменение звена ломаной может привести к изменению ее формы и свойств. Поэтому при решении задач и графическом представлении данных необходимо учитывать данную особенность

Что такое угол наклона ломаной линии

Ломаная линия – это линия, которая состоит из отрезков, соединенных в углы. Углы при этом могут быть любыми: острыми, прямыми или тупыми. Угол наклона ломаной линии – это угол, который образуется между наклоном каждого отрезка и горизонтальной осью координат.

Угол наклона может быть положительным или отрицательным и может быть любым числом. Если угол наклона положительный, то ломаная линия растет, если отрицательный, то она падает. Угол наклона ломаной линии также позволяет нам определить, как быстро растет или падает линия.

Угол наклона ломаной линии является важным понятием в математике и используется в различных областях, таких как наука о данных, экономика и финансы. Он также может быть использован для описания ландшафта, расчета скорости движения автомобилей или любых других объектов, перемещающихся по линии.

Для расчета угла наклона ломаной линии необходимо найти разницу между координатами конца и начала каждого отрезка по оси y и x, затем разделить значение по оси y на значение по оси x. Это даст нам тангенс угла наклона. Измерение угла производится в градусах, минутах и секундах, обычно выражая в виде десятичной дроби.

Определение угла наклона ломаной линии важно при построении графиков и графическом отображении данных. Понимание концепции угла наклона также поможет студентам быстро и легко решать задачи связанные с ломаными линиями

Задачи на построение и расчеты с использованием ломаных линий

Ломаные линии не только могут быть построены для визуального представления информации, но и использоваться при решении задач. Рассмотрим несколько примеров задач на построение и расчеты с ломаными линиями:

• Задача 1: На плоскости даны точки A, B, C, D, E. Постройте ломаную линию, проходящую через все эти точки в порядке их расположения. Рассчитайте длину этой линии.
• Задача 2: Для проведения газопровода необходимо соединить точки A и B, при условии, что максимальный угол между соседними участками газопровода не должен превышать 45 градусов. Постройте оптимальную ломаную линию между точками A и B.
• Задача 3: Ломаная линия задана координатами вершин: A(1,1), B(3,5), C(5,2), D(7,5). Найдите длину этой ломаной линии и расстояние от точки A до линии.

Все эти задачи требуют использования знаний о построении ломаных линий и решении геометрических задач

При решении таких задач очень важно внимательно следить за последовательностью точек, чтобы линия была построена корректно и учесть все даные, например, максимальный угол между участками ломаной

Знания о ломаных линиях позволяют решать множество задач не только в геометрии, но и в других областях знаний, например, при моделировании процессов в экономике, физике и других науках.

Что такое ломаная линия 1 класса?

Ломаная линия 1 класса – это геометрическая фигура, составленная из отрезков, соединяющих точки на плоскости. Все отрезки имеют общее направление и не пересекаются. Она также называется полигоном.

Как построить ломаную линию 1 класса?

Чтобы построить ломаную линию 1 класса, необходимо провести на плоскости отрезки, соединяющие точки, расположенные на одной прямой, в одном направлении. Начертите точки на листе бумаги, соедините их отрезками и получите линию.

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

Вершинами ломаной линии называются концы отрезков , из которых она состоит.Звеньями ломаной линии называются составляющие ее отрезки .Смежные звенья – это звенья, которые имеют общие вершины .Смежные звенья не могут принадлежать одной прямой.Длина ломаной линии – это сумма длин всех входящих в ее состав звеньев.

На рисунке 12 видно, что:

• KLMN – ломаная линия;
• K, L, M, N – вершины ломаной KLMN;
• KL, LM, MN – звенья ломаной KLMN;
• KL и LM – смежные звенья;
• LM и MN – смежные звенья;
• KL и MN – не являются смежными звеньями.

Называют ломаную линию по названию ее вершин, соблюдая их последовательность. Так, называть ломаную на рисунке 11 как KLMN или NMLK – правильно , а MLKN или MNLK – не правильно .

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Название разомкнутой ломаной начинается с названия вершины, с которой она начинается. Замкнутую ломаную можно называть , начиная с любой ее вершины.

• ABCDE — замкнутая ломаная;
• FGHKLM — разомкнутая ломаная

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

На рисунке 13 у замкнутой ломаной ABCD два пересекающихся звена: BC ∩ DA , а у разомкнутой ломаной EFGHI – три: EF ∩ HI и FG ∩ HI .

Чтобы нарисовать геометрическую фигуру правильно, нужно знать теорию. Ломанная линия состоит из прямых отрезков, которые между собой последовательно соединены. Для закрепления знаний нужна практика. Предлагаем Вашему вниманию набор картинок с изображениями ломанных линий.

Ломаная линия из четырёх звеньев.

Картинка с описанием ломаных линий.

Ломаная из трех звеньев рисунок 1 класс.

Изображение на урок математики.

Вершины ломаной линии 1 класс рисунок.

Прикольное задание для школьников младших классов.

Детские рисунки.

Из разного количества звеньев.

Ломаная из четырех звеньев рисунок 1 класс.

Пример ломаной линии для детей.

Задание для учеников младших классов.

Самая простая ломаная линия.

Из двух звеньев.

Ломаные линии составлены из отрезков. У ломаной линии конец одного отрезка — начало другого, кроме концов ломаной.

Первый вариант не подходит, потому что присутствуют кривые линии. У ломаной линии отрезки прямые.

Второй вариант — ломаная линия. Отрезки не принадлежат одной прямой и из конца следующего отрезка выходит новый отрезок.

Третий вариант не подходит, потому что это прямая линия — все отрезки лежат на одной прямой.

Задание 2.

Начерти в тетради ломаную из трех звеньев. Сколько у нее вершин? Начерти ломаную из трех звеньев с тремя вершинами. Какая фигура получилась?

Пояснение:

У нарисованной ломаной 2 вершины.

Пояснение:

У нарисованной ломаной 3 вершины. Получился треугольник.

Задание 3. Задание на полях.

У верхних фигур количество вершин и звеньев разные, а у нижних фигур количество вершин и звеньев одинаковое.

Пояснение:

Считаем звенья.

На первом изображении у красной фигуры 5 звеньев; у синей фигуры 4 звенья.

На втором изображении у зеленой фигуры 4 звенья; у оранжевой фигуры 5 звеньев.

Считаем вершины.

На первом изображении у красной фигуры 4 вершины; у синей 3 вершины.

На втором изображении у зеленой фигуры 4 вершины; у оранжевой фигуры 5 вершин.

Получайте уведомления о выходе новых решебников и примите участие в ежемесячном розыгрыше.

• Как сделать карту поляка в беларуси в 2021 году

    

• Как сделать так чтобы сон повторился

    

• Как сделать скринсет для mach3

    

• Как сделать умывальник из канистры на фуру

    

• Как сделать кунай из металлического конструктора

Рисунок и объяснение ломаной из трех звеньев с определенным количеством вершин

Количество вершин в ломаной из трех звеньев может быть различным. В зависимости от числа вершин, ломаная может иметь разную форму и структуру. Рассмотрим несколько примеров:

Число вершин	Рисунок ломаной
1
2
3
4
5

На рисунках представлены ломаные из трех звеньев с разным количеством вершин. В первом примере есть только одна вершина, поэтому ломаная представляет собой прямую линию. Во втором примере есть две вершины, поэтому ломаная состоит из двух прямых линий, образующих один угол. В третьем примере есть три вершины, поэтому ломаная имеет два угла и образует букву «П».

Чем больше вершин в ломаной, тем сложнее ее форма и структура. В зависимости от задачи, ломаная может быть использована для представления различных линий или границ объектов. Также она может использоваться для визуализации данных или построения графиков.

Ломаная линия — как элемент компьютерной графики

Многие мамы огорчены зависимостью детей от гаджетов. Но можно использовать увлечение во благо. К примеру, рассказать ребёнку, что в компьютерной графике ломаные линии широко используются для создания различных 3D-объектов и анимаций. Они представляют собой набор вершин, то есть точек, соединенных отрезками, то есть ребрами. Используя различные алгоритмы, можно создавать сложные трехмерные модели, состоящие из миллионов вершин и ребер.

Ломаные линии играют важную роль в создании анимаций, так как они позволяют моделировать движение объектов и изменение их формы во времени. Например, можно создать анимацию автомобиля, который движется по дороге, используя ломаные линии для моделирования движения колес и кузова автомобиля.

Одним из наиболее распространенных способов использования ломаных линий в компьютерной графике является создание полигональных моделей. Полигональная модель – это трехмерный объект, состоящий из множества многоугольников, каждый из которых представляет собой ломаную линию с тремя или более вершинами. Такие модели могут быть визуализированы с использованием различных методов, таких как растеризация, трассировка лучей или применение эффектов глубины резкости.

Также ломаные линии используются в алгоритмах визуализации для определения того, какие объекты находятся ближе или дальше друг от друга. Это позволяет создавать реалистичные изображения и анимации с учетом глубины сцены.

Собрали интересные задания на ломаные линии, которые изменят представления вашего ребенка о скучной математике здесь. Регистрируйтесь на платформе iSmart и начинайте заниматься.

Выберите полотно и инструменты

Перед тем как начать рисовать ломаную с 3 звеньями и 3 вершинами, вам необходимы следующие материалы и инструменты:

• Лист бумаги формата А4 или большего размера;
• Карандаш для набросков или мягкий грифельный карандаш;
• Линейка;
• Резинка.

Выберите плоскую поверхность для работы, чтобы обеспечить комфортное положение руки и доступность всех необходимых инструментов.

Хорошо заточенный карандаш поможет вам создать четкие и аккуратные линии, поэтому убедитесь, что вы подготовили его к использованию.

Линейка даст возможность рисовать прямые линии с той точностью, которая требуется для нашей задачи. Убедитесь, что линейка полностью прямая и не повреждена, чтобы избежать искажений при выполнении рисунка.

Резинка поможет вам исправить ошибки и стереть наброски, которые больше не нужны. Выберите мягкую и хорошо стирающуюся резинку, чтобы не повредить бумагу.

Важные особенности при нахождении вершин

При нахождении вершин в ломаной 1 класса необходимо учесть несколько важных особенностей:

1. Ломаная 1 класса состоит из отрезков, каждый из которых соединяет две вершины. Поэтому необходимо проверить каждый отрезок на пересечение с остальными отрезками, чтобы точно определить местоположение вершин.
2. Если ломаная содержит изогнутый отрезок, то необходимо разбить его на несколько прямых отрезков. При этом для каждого прямого отрезка необходимо выполнить проверку на пересечение с остальными отрезками.
3. Ломаная 1 класса может содержать вершины, которые находятся на одной прямой. Эти вершины являются одной вершиной ломаной и должны быть учтены при нахождении остальных вершин.
4. При нахождении вершин необходимо проверять все возможные комбинации точек, чтобы исключить возможность пересечения отрезков или их повторного использования.
5. Если ломаная 1 класса имеет петли или самопересечения, то необходимо произвести дополнительные проверки и разделить ломаную на несколько частей. Каждая часть будет иметь свои вершины, которые необходимо отдельно определить.

Учет этих особенностей позволит точно определить вершины ломаной 1 класса и построить ее правильную структуру.

Особенности построения многоугольников

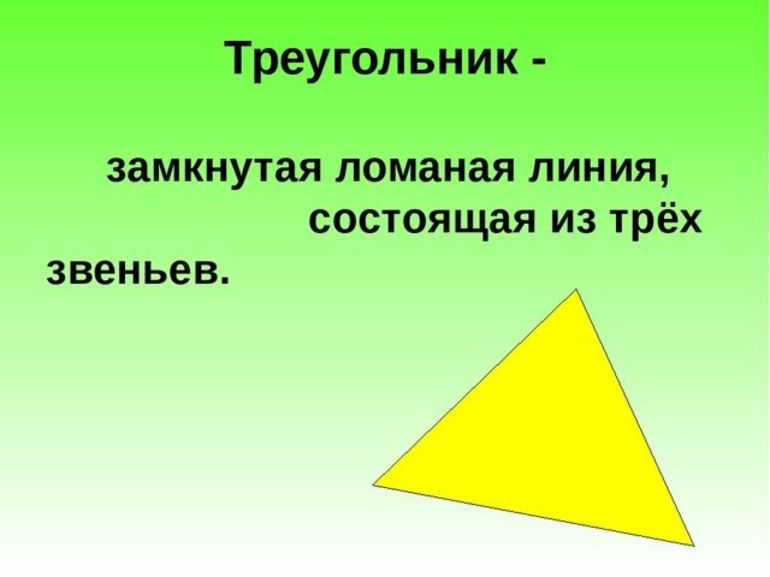
В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.

Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.

Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.

Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:

1. Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
2. Равносторонние. Абсолютно все стороны обладают идентичной длиной.
3. Специфические остроугольные. Сформированные углы имеют острую форму.
4. Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
5. Тупоугольные. Фигура обладает одним тупым углом.
6. Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.

Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.

Практические советы по изучению ломаных для детей в 2 классе

Ломаные линии – это важный элемент математики. Их нужно уметь правильно читать и рисовать, чтобы решать задачи. Вот несколько советов, как научиться работать с ними:

• Начните с простых ломаных, которые содержат всего несколько углов. Это поможет ребенку научиться их правильно расставлять и не мешать им друг друга.
• Попросите ребенка нарисовать ломаную, используя геометрическую сетку. Это гарантирует правильность построения линий и углов.
• Добавьте сложности, такие как перевернутые углы или повороты линии, постепенно. Не наваливайте слишком много сложности за один раз.
• Предложите ребенку решать задачи, включающие использование ломаных линий для вычислений. Это поможет закрепить знания и умения.
• Поощряйте ребенка, когда он делает успехи. Это поможет ему чувствовать себя уверенно и продолжать учиться.

Следуя этим простым советам, ребенок научится работать с ломаными линиями легко и быстро, что сделает его уверенным в математике и поможет ему решать задачи эффективно.

Какие бывают ломаные вообще?

Ломаная – это линия, состоящая из отрезков, которые соединяют точки на плоскости. Она может иметь любую форму и количество углов, но обычно ломаные делят на простые и сложные. Простая ломаная состоит из отрезков, в которых нет пересечений, а сложная имеет пересекающиеся линии.

Как определить, что ломаная имеет угол?

Если линия сделана из более чем двух отрезков и угол в котором пересекаются два отрезка не равен 180 градусам, то это ломаная с углом.

Что такое ломаная линия в математике?

Ломаная линия – это геометрическая фигура, которая состоит из последовательности отрезков, соединяющих точки на плоскости.

Каковы основные свойства ломаных?

Основные свойства ломаных: длина отрезка между двумя точками на ломаной не может быть больше, чем длина ломаной между соседними точками; ломаная может быть представлена как сумма векторов, имеет длину и направление, а также угол между соседними векторами определяет форму угла на ломаной.

Какие бывают ломаные 2 класс?

Ломаные 2 класса – это простые ломаные, которые состоят из отрезков, соединяющих точки на плоскости, не имеют пересечений и углов меньше или равных 180 градусам. Ломаные 2 класса могут быть представлены в виде направленной последовательности точек с координатами (x, y).

Как находить длину ломаной?

Длина ломаной – это сумма длин всех отрезков, из которых состоит ломаная. Для нахождения длины ломаной нужно посчитать длину каждого отрезка и сложить их.

Как строится график ломаной на координатной плоскости?

График ломаной на координатной плоскости строится следующим образом: на плоскости отмечаются точки с координатами (x_i, y_i), которые соединяются отрезками. Полученная последовательность отрезков задает ломаную. График ломаной получается как набор последовательных отрезков, заданных координатами своих концов.

Удаление звена ломаной

Удаление звена ломаной представляет собой операцию, при которой одно из звеньев ломаной пропускается или удаляется. Это позволяет изменить форму и длину ломаной.

Для удаления звена необходимо определить, какое именно звено нужно удалить. Обычно, для удобства, звенья ломаной пронумерованы. Чтобы удалить нужное звено, его номер указывается в соответствующем алгоритме или задаче.

Удаление звена ломаной может быть полезным при решении различных задач. Например, если требуется изменить форму ломаной таким образом, чтобы она проходила через определенные точки или обладала определенным свойством.

При удалении звена ломаной необходимо учитывать, какие влияния это может иметь на ее свойства. В частности, удаление одного звена может изменить ее длину, форму или направление. Поэтому перед удалением звена стоит тщательно продумать, как это повлияет на остальную ломаную и решение задачи в целом.

Пример: Рассмотрим ломаную, состоящую из следующих звеньев: A, B, C, D. Предположим, требуется удалить звено B. После удаления звена B, ломаная будет состоять из звеньев A, C, D.

Как работать с координатами точек на ломаной линии

Для работы с координатами точек на ломаной линии необходимо знать, как задаётся эта линия. Ломаная линия задаётся последовательностью упорядоченных пар координат (x, y), где x — это координата по оси абсцисс (горизонтальная ось), а y — это координата по оси ординат (вертикальная ось).

Чтобы определить координаты точки на ломаной линии, нужно сначала понять, на каком отрезке линии она находится. Для этого можно использовать метод интерполяции, который заключается в нахождении координат точки на отрезке между двумя заданными точками и задействует соотношение между расстояниями на осях координат.

Когда находятся координаты точки на отрезке, можно найти ее общие координаты, используя соотношения между расстояниями на осях координат для всей ломаной линии.

Также можно использовать таблицу координат точек на ломаной линии. В этой таблице указаны координаты каждой точки на линии и на каких отрезках они расположены. Это может значительно упростить работу с координатами и избежать ошибок при нахождении координат.

Нумерация точек на ломаной линии часто начинается с 1. Также можно использовать название каждой точки для более удобной работы.