Как объяснить дроби ребенку?

Умножение и деление обыкновенных дробей

Прежде чем приступить к изучению вопроса об умножении и делении дробей, вспомним, что такое натуральные числа? А это те, которые начинаются с единицы – 1 и продолжаться могут до бесконечности. Но, к ним относятся только положительные числа, т.е, со знаком “+”. Числа: -1; -2; -3; -4; -5 и т.д., натуральными не являются.

Для того, чтобы совершить действие умножения, нужно умножить числитель одной дроби на числитель другой и, соответственно, перемножить знаменатели. Что у нас получается? В результате вычисления (умножения) мы получаем дробь с числителем, который равен произведению числителей в дробях, и со знаменателем, равным произведению в дробях знаменателей.

Пример:

Умножается число 3 на число 7 (числители).  Умножаются знаменатель 5 на знаменатель 10. Записать данное действие можно двумя способами, это вы видите на картинке.

Пример умножения целого числа и дроби:

Целое число (2) записывается в виде дроби (2/1), в которой знаменателем будет единица (1).

Если нужно произвести деление дробей, поступают следующим образом: умножают первую дробь на перевернутую вторую.

Для простоты восприятия воспользуемся правилом сокращения: делим делитель и знаменатель на одинаковое число, например, дробь 21/63 выглядит не очень хорошо для восприятия, гораздо понятнее будет так – 1/3.

Делим смешанные числа:

Сначала их нужно представить неправильными дробями, затем, разделить друг на друга, вот, что получилось:

Пример:

Дроби: с чего начать?

Начать нужно с повторения предыдущего материала. Если быть точнее – нужно вспомнить основные математические действия с целыми числами: сложение, вычитание, умножение, деление. Все эти знания формируются в дошкольном и младшем школьном возрасте, и без них решать примеры с дробями не представляется возможным. Если с этими действиями проблем нет, то нужно объяснить ученику, чем вообще являются дроби.

Говоря доступным для ребёнка языком, дробь – это часть чего-либо. Это самое «что-либо» может быть всем, чем угодно: тортиком, апельсином, начерченным на бумаге кругом. Иногда часть какого-то предмета называют долей. Но при этом суть понятия не меняется: этот самый предмет дробят, делят на части.

Понять значение этого действия гораздо проще на наглядных примерах. Так, можно взять пирог и разрезать (то есть разделить) его на несколько равных частей. Один кусок будет считаться одной долей от целого пирога. Если пирог разделён на четыре части, то один кусочек – это одна четвертая. Если на восемь, то одна восьмая часть.

Помните мультик, где герои делили апельсин?

«Мы делили апельсин.

Много нас, а он один.

Эта долька для ежа, эта долька для чижа…»

В этой нехитрой песенке как раз объясняется принцип деления на доли, или дробление. То же самое можно проделать с яблоком, плиткой шоколада или конфетами из вазы. Общее количество конфет – это целое, а одна конфетка – это часть.

Дроби: как это оформить?

Обыкновенная дробь – это понятие будет регулярно встречаться школьникам почти на каждом уроке математики, поэтому нужно сразу разобраться с тем, что оно обозначает и как используется на практике. Начнём со второй части: обыкновенная дробь используется для записи любого количества долей. Выглядит она как «двухэтажная» конструкция из двух чисел, разделённых горизонтальной чертой. Эта черта называется дробной и обозначает, что число разделили.

Верхний «этаж» называется числителем,

нижний – знаменателем.

Числитель – это число взятых частей от целого, а знаменатель – количество частей, на которое разделили целое. Кстати, знаменатель можно записывать не только внизу, но и справа от числителя после дробной черты. Например: 1/3 или 2/6 или 4/8.

А теперь снова вернёмся к нашему вкусному пирогу. Уже понятно, что разделить его можно между любым количеством друзей. Соответственно, число всех нарезанных кусочков мы запишем в знаменатель. А количество кусков, доставшихся, например, Пете, мы запишем в верхней части, то есть в числителе. Если пирог порезали на восемь частей, а Петя съел два из них, то запись будет выглядеть так: 2/8. А если поделить яблоко между двумя товарищами, то каждому достанется по одной второй, или ½.

Правильные и неправильные дроби

Наверное, вы уже обратили внимание, что во всех приведённых примерах числитель меньше знаменателя. Это называется правильной дробью

Но ведь бывают и другие ситуации. Например, к Маше пришла в гости подруга Лена, и мама Маши решила угостить девочек фруктами. Одна достала из холодильника два яблока и, чтобы им было удобнее, разрезала каждое пополам. Получается следующее: одно яблоко разделено на две части, значит в знаменателе будет два. Один кусочек этого самого яблока – это одна вторая. То же самое и со вторым яблоком. А всего на тарелке лежит четыре кусочка.

Но только вот Лена не очень любит яблоки. Она съела всего лишь один кусок, а все остальные достались Маше. Получается, что на долю Лены пришлась ½ часть, а у Маши 3/2. Это и есть неправильная дробь,

то есть та, в которой числитель больше знаменателя.

Иногда в математических примерах могут встретиться ещё более странные записи: 1/1, 3/3, 5/5. Это тоже неправильные дроби, которые по сути не совсем соответствуют определению дробных чисел. И снова вернёмся к сочному и спелому яблоку и рассмотрим на его примере число 2/2. Знаменатель указывает на то, что яблоко разделено на две части, а числитель говорит о том, что Маша съела обе. То есть она съела всё яблоко, а это значит, что дробное число 2/2 = 1. Если пирог разделён на три части и все они достались Пете, то он смог полакомиться целым пирогом: 3/3 = 1.

Презентация на тему: » «Что мы знаем о дробях» Цели урока: повторить, обобщить и закрепить знания учащихся об обыкновенных дробях и действиях с ними; способствовать развитию.» — Транскрипт:

1

«Что мы знаем о дробях» Цели урока: повторить, обобщить и закрепить знания учащихся об обыкновенных дробях и действиях с ними; способствовать развитию умения решать примеры на все действия; проверить степень усвоения учащимися материала в ходе проверочной самостоятельной работы.

2

Математику уже затем учить надо, что она ум в порядок приводит. (М.В.Ломоносов)

3

Приведение дробей к общему знаменателю Сравнение дробей Сложение и вычитание дробей Умножение дробей Деление дробей

4

Приведение дробей к одному знаменателю Чтобы привести дроби к одному знаменателю надо: найти наименьший общий знаменатель(НОЗ) данных дробей; найти дополнительный множитель к каждой дроби(для этого надо НОЗ разделить на знаменатели данных дробей); найти «новые» числители(для этого дополнительные множители умножить на числители данных дробей). Чтобы найти НОЗ надо: перемножить знаменатели данных дробей, если они взаимно просты, например, взять в качестве НОЗ больший знаменатель, если он делится на меньший, например, взять в качестве НОЗ НОК знаменателей данных дробей, например,

5

Из двух дробей с одинаковым знаменателем та дробь больше, у которой числитель больше, и та дробь меньше, у которой числитель меньше, например, Из двух дробей с одинаковым числителем та дробь больше, у которой знаменатель меньше, и та дробь меньше, у которой знаменатель больше, например, При сравнении дробей с разными знаменателями надо: 1. привести дроби к одному знаменателю; 2. сравнить дроби по выше изложенному правилу, например,

6

При сложении или вычитании дробей с одинаковыми знаменателями надо сложить или вычесть их числители, а знаменатель оставить без изменения, По возможности полученную дробь сократить. При сложении или вычитании дробей с разными знаменателями надо привести дроби к одному знаменателю, а затем работать по предыдущему правилу.

7

При умножении обыкновенных дробей надо числитель одной дроби умножить на числитель другой дроби, знаменатель умножить на знаменатель, сократить полученную дробь, если это возможно, например:

8

При делении обыкновенных дробей надо делимое умножить на дробь, обратную делителю: Например,

9

Выполните задания. Решить на доске и в тетрадях : 6(а; в; д), 7(б, г), 8(а). Решить на доске и в тетрадях : 9 (а,в,д,ж,и), 10(а,в,д,ж) Решить на доске и в тетрадях : 11(б,г,е,з,к,м), 12(1 и 3 столб.) Решить на доске и в тетрадях : 20.

10

Вариант 1 1. Вариант 2

11

п. 1.1, 6(в,д), 7(а, в), 9(б,е), 10(б,г), 11(а,в,ж,и), 12(2 ст. ) Домашнее задание.

Перевод обыкновенных дробей в десятичные

Обыкновенные дроби представляют собой дроби, которые имеют числитель и знаменатель. Для того чтобы перевести обыкновенную дробь в десятичную, необходимо разделить числитель на знаменатель.

Многие обыкновенные дроби имеют десятичное разложение, которое может быть представлено как конечная или бесконечная десятичная дробь. Для того чтобы получить десятичную дробь, нужно разделить числитель на знаменатель, используя десятичную точку.

Например, если мы хотим перевести обыкновенную дробь 3/4 в десятичную, нам нужно разделить 3 на 4:

3 ÷ 4 ≈ 0.75

Таким образом, 3/4 в десятичном виде будет 0.75.

Если результат деления числителя на знаменатель имеет бесконечную десятичную дробь, то следует округлить его до заданного количества знаков после десятичной точки.

Например, обыкновенная дробь 1/3 имеет бесконечную десятичную дробь:

1 ÷ 3 = 0.33333333…

Для округления до двух знаков после десятичной точки, нужно зафиксировать два первых знака после десятичной точки и добавить к ним единицу, если следующий знак больше или равен 5. Таким образом, 0.33 + 0.01 = 0.34, и дробь 1/3 в десятичном виде будет 0.34.

Надеемся, что данная информация поможет вам переводить обыкновенные дроби в десятичные и понимать их значение.

Минутка истории

Точное время появления дробных выражений пока не установлено. Но исторические находки предполагают, что они возникли в связи с жизненной необходимостью. Задания с использованием дробей считались самыми сложными, и выполнять их могли, только люди, обладающие огромным умственным потенциалом. За такие знания, мудрецов почитали на уровне бога. Ведь без их помощи невозможно было разделить добычу между всеми охотниками поровну, уловмежду рыбаками, урожай между соседями. До сих пор в Германии существует поговорка «Оказаться в дробях», – это значит попасть в попасть в непонятную, запутанную ситуацию.

На Русь, понятие «дробь»пришлов начале 9 века. Источником этого понятия стало выражение «дробить» (разделять, разламывать). На протяжении длительного времени,разные народы называли такие числа ломаными, ведь при разделении любого предмета (конфета, яблоко, хлеб) его приходилось разламывать.

В России существовала отдельная единица измерения для определения размеров земельных наделов, она состояла из четверти и получетверти. Еще эту единицу называли осьмина. Это была дробь, которая использовалась только для измерения земельных угодий. Осьминой невозможно измерить другие величины, скорость или количество прибыли. Гораздо позже эта единица измерения преобразовалась в 1/8, которую можно применять для измерения любой величины.

В произношении дробных чисел на Руси, были свои правила. В название, дробного числа,знаменатель которого больше 5, и меньше 11 добавлялось окончание «ина»: 1/6– шестина, 1/9– девятина, 1/10– десятина. Если дробь имела в знаменателе число больше 10, то в названии дроби обязательно произносились слово «жеребей»: 4/13 – четыре тринадцатых жеребьев.

Число, которое записывалось над чертой, называли верхнее число, а число под чертой – исподнее число.

Где в жизни мы можем встретить дроби:

— При использовании мер измерения: 1 грамм=1/1000 килограмма=1/100000 центнера

— Охотники,используют дробь.

— В медицине. Каждое лекарственное средство, в своем составе, содержит различные компоненты, измеряющиеся дробями.

— Быструю, резкую игру на барабанах называют барабанной дробью.

— По команде капитана корабля «дробь» сразу прекращается огонь.

— При нумерации домов использование дробей уместно на двух пересекающихся улицах.

— Основными движениями в русских народных танцах является дробь и бег.

— Во всех кулинарных рецептах, необходимые пропорции указаны дробными числами: 2/3 стакана муки или 3/4 яблока.

Действия с дробями

В самом начале мы говорили, что горизонтальная черта в записи дроби означает деление. То есть числитель можно разделить на знаменатель. Рассмотрим пример с неправильной дробью 6/3. Мы 6 делим на 3 и получаем в ответе 2. Ещё один пример – 8/4: 8 делим на 4 и получаем 2.

В этих примерах в итоге получается целое число без остатка. Но бывает и по-другому, и называется это действие «выделение целой части».

Выделение у дроби целой части

Для примера возьмём неправильную дробь 7/2 и попробуем её разделить:

7 : 2 = 3 и 1 в остатке.

Выполним обратное действие и проверим правильность решения:

3 х 2 + 1 = 7

Теперь осталось записать. А делается это очень просто: целая часть записывается крупно слева от дроби, а сама дробь будет выглядеть как остаток в числителе и количество частей в знаменателе: 3 ½

Кстати, то, что мы сейчас получили, называется смешанной дробью. У неё есть целая и дробная часть. Но подобные действия можно выполнить только с неправильными дробями, у которых числитель больше знаменателя. В математике используется и обратное действие: перевод смешанной дроби в неправильную. Но эти действия, скорее всего, вы будете изучать позже – в 6 классе.

Сравнение дробей

А на данном этапе сосредоточимся на более простых задачках. Например, научимся сравнивать дроби. Сравнить их можно только, если они имеют одинаковый знаменатель. По правилам математики сравниваются числители.

Что больше – 1/5 или 4/5? Сравним числители и увидим, что 1 < 4, а значит 1/5 < 4/5.

А если в примере дробные числа с разными знаменателями? Тогда их сначала нужно привести к общему, а потом сравнить. Но это более сложная тема, требующая детального разбора. Как и другие примеры с умножением, делением, сокращением. А пока достаточно общего представления о дробях.

Понятие доли и обыкновенной дроби

Новый год – любимый праздник многих. Дед мороз, праздничный стол, подарки, веселье. Ассоциации у всех разные. И только мандарин, вызывает у каждого праздничное настроение.

Изображение взято с фотостока 

Вот именно на примере мандарина и рассмотрим, что такое доли.

Представьте, что праздники закончились, а в вазе остался только один мандарин. Как же разделить его на всех, как сделать так, чтобы все получили одинаковую долю?

Очень просто! Мандарин следует поделить на дольки, и раздать желающим.

На рисунке, фрукт состоящий из 8 долек, то есть 8 человек могут взять по 1 дольке. Делаем вывод, что доля – это одна из одинаковых частей чего-либо. Каждый гость получил по 1 из 8 долек, значит, получил по 1/8 всего мандарина.

Если бы гостей было двое, то фрукт пришлось делить на 2 части, при этом, каждый взял бы по однойиз двух половинок, то есть по ½ мандарина или половину.

Запомни!1/2 – половина,1/3 часть называют – треть, а ¼ – четверть.

Например:яблоко разрезали на 3 кусочкаи раздали 3 детям, получается, что каждому ребенку досталась треть яблока.

Для письменного обозначения количества долей, используются обыкновенные дроби.В записи которой, содержится два числа и черта, которая их разделяет. Черта бывает горизонтальной и вертикальной.

5Например: 4/9 или 8

 Помни! Обыкновенная дробь – число вида c/k, где обязательно с и к натуральные числа.

6  2Например: 11/15, 7, 3

Числовое значение, расположенное над чертой, или слева от неё, называют числителем. Числителем обыкновенной дроби c/k называют натуральное число с.

Числовое значение, расположенное под чертой или справа от неё, называют знаменателем.

Знаменателем обыкновенной дроби c/k, называют натуральное число к.

Давайте разберемся, какую информацию несет числитель и знаменатель?

Запомни! Знаменатель указывает на количество равных долей в предмете.

Например: в дробном числе 5/6, знаменатель 6 говорит, что предмет состоит из 6 долей.

Запомни! Числитель показывает, количество используемых долей.

Например: в записи 5/6, числитель 5 показывает, что используется 5 долей.

Получается, 5/6 говорит о том, что предмет разделен на 6 долей, но используется только 5 из них.       

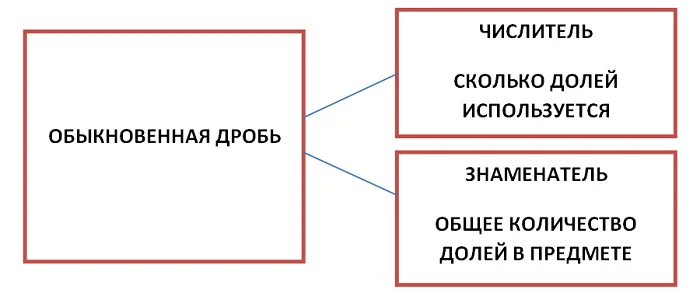
Если пока не получается запомнить из каких компонентов состоит дробь, то просто сохрани табличку и пользуйся!

Теперь давайте рассмотрим, как же выполнить сравнение обыкновенных дробей.

Представим такую ситуацию:

Мама испекла пирог и разделила его на 3 части. Дети съели лакомство. Миша съел 2/3 пирога, а Васе досталась 1/3. Как определить, кому достался больший кусок пирога?

На рисунке видно, что порция Миши оказалась больше.

Значит, 2/3>1/3.

Сформулируем правило сравнения обыкновенных дробей.

Помни! Чтобы сравнить дроби, имеющие равные знаменатели, достаточно сравнить только числители. Больший числитель соответствует большему числу.

Например:

4    59 < 9, 8/11 > 6/11

Довольно часто, возникает необходимость, найти сумму или разность обыкновенных дробей. Как правильно выполнять действия сложения и вычитания обыкновенных дробей?

Рассмотрим сложение дробей:

Назару задали 15 примеров, он сначала решил 2 примера, а потом ещё 1 пример. Мама поинтересовалась у него, какая часть домашнего задания выполнена? Назар задумался. Давайте подумаем и мы:

Все задание состоит из 15 примеров – это количество долей, на которое разбито все задание, или знаменатель. Сначала мальчик вычислил 2 примера – это часть задания, которая взята к рассмотрению, или числитель. Получаем 2/15. Позже он решил еще один пример, значит, выполнил еще 1/15 всей работы. Чтобы определить, какая часть задания выполнена, необходимо сложить полученные выражения: 2/15 + 1/15.

Помни! При сложении обыкновенных дробей, достаточно суммировать числители, а цифру под чертой записать без изменений.

2/15 + 1/15 = (2+1)/15 = 3/15.

Получается, что мальчик выполнил 3/15 всего задания, значит, 3 задания из 15.

Теперь давайте узнаем, как необходимо выполнять вычитание обыкновенных дробей, имеющих равные знаменатели.

Важно! Чтобы найти разностьдвух дробей, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель записать без изменений. Например: 5/8 — 2/8 = (5-2)/8 = 3/8

Например: 5/8 — 2/8 = (5-2)/8 = 3/8

Деление дробей

Деление. А что деление? Деление это действие обратное умножению. Сейчас поясню, существует такое понятие, как «обратная дробь», или дробь обратная данной, иными словами, это попросту перевернутая дробь! 

Смотри: \( \displaystyle  \frac{1}{7}:\frac{3}{5}=\frac{1}{7}\cdot \frac{5}{3}=\frac{5}{21}\)

Как ты видишь, дробь \( \displaystyle  3/5\) просто переворачивается, а знак деления меняется на умножение!

А деление дроби на число или наоборот особо не отличается от деления на дробь, ведь любое число можно представить виде дроби – как, спросишь ты?

А ты знаешь, сколько будет \( \displaystyle  7/1\), например? По сути это \( \displaystyle  7\) пирогов разделить на одного человека. Сколько пирогов получит он? Семь!

Значит, \( \displaystyle  7:\frac{3}{5}=\frac{7}{1}\cdot \frac{5}{3}=\frac{35}{3}=11\frac{2}{3}\).

Дроби на числовой прямой

Числовая прямая — графическое изображение числовой оси, на которой можно изобразить любое число, в том числе и дробь.

Для изображения дроби на числовой прямой используются точки. В числителе дроби ставится точка на нужное количество делений правее нуля, в знаменателе — на таком же расстоянии, но слева от нуля. Например, для дроби 3/4 в числителе на числовой прямой ставится точка после трёх делений, а в знаменателе — точка перед четырьмя делениями.

Если дробь отрицательная, то точка помещается справа от нуля в числителе и слева от нуля в знаменателе. Например, для дроби -2/5 в числителе точка будет стоять после двух делений справа от нуля, а в знаменателе — перед пятью делениями слева от нуля.

Таким образом, изображение дроби на числовой прямой позволяет увидеть ее положительность или отрицательность, а также составить представление о ее величине и соотношении с другими дробями и числами на числовой прямой.

Вычитание дробей

Вычитание дробей практически ни чем не отличается от сложения, ну разве что знаком. А так, вычитается знаменатель из знаменателя, при сохранении общего числителя неизменным, а в случае если знаменатели разные, дроби приводятся к общему знаменателю.

Но куда же без специфики, тут она тоже присутствует.

Что-нибудь понятно хоть чуточку? – Ладно, смотри пример, сейчас разберешься!

\( \displaystyle  4\frac{1}{3}-2\frac{2}{3}=3\frac{4}{3}-2\frac{2}{3}=1\frac{2}{3}\) – как ты видишь, в дробной части, тут из \( \displaystyle  1/3\) вычитается \( \displaystyle  2/3\).

Но, очевидно, что, не привлекая «кусочки» от целого пирога, вычитание совершить нельзя. Для этого один пирог режут на куски и добавляют их к дробной части.

Получается, что уже из \( \displaystyle  4/3\) вычитают \( \displaystyle  2/3\), а тут уж нет проблем.

А с десятичными дробями все то же самое, что и было при сложении.

Вот тебе пример:

Как объяснить ребенку дроби

Не ждите, пока ребенок пойдет в 5 класс и встретится с дробями на страницах учебника по математике. Ответ на вопрос «Как объяснить ребенку дроби» рекомендуем поискать на кухне! И сделать это прямо сейчас! Даже если вашему малышу только 4-5 лет, смысл понятия «дроби» он в состоянии уяснить и даже может научиться простейшим действиям с дробями.

Мы делили апельсин. Много нас, а он одинЭта долька для ежа, эта долька для чижа…А для волка — кожура.

Помните стихотворение? Вот самый наглядный пример и самое эффективное руководство к действию! Объяснить ребенку дроби проще всего на примере еды: режем яблоко на половинки и четвертинки, делим пиццу между членами семьи, разрезаем буханку хлеба перед обедом и т.п. Главное, перед тем, как съесть «наглядное пособие» не забудьте озвучить, какую часть от целого вы «уничтожаете».

Сделайте акцент на том, что ЦЕЛЫЙ апельсин (яблоко, шоколадка, арбуз и пр.) — это 1 (обозначаем цифрой 1).

Апельсин или шоколадку мы делим, можно еще сказать «дробим» на несколько частей.

Покажите ребенку хорошо знакомый предмет — линейку. Объясните, что между числами есть промежуточные значения — части.

i.ytimg.com

Объясните, как записывать дроби: что значит числитель, и на что указывает знаменатель.

Смысл понятия «дроби» и правильную запись легко показать на примере конструктора. В числителе НАД чертой пишем какая часть, а в знаменателе ПОД чертой — на сколько таких частей было разделено целое.

gladtolearn.ru

Обязательно на наглядном примере покажите разницу между дробями с одинаковым числителем, но разными знаменателями.

gladtolearn.ru

На примере 4-х квадратов одинакового размера покажите, как можно разделить их на одинаковое/разное количество частей. Пусть ребенок сам разрежет ножницами бумажные заготовки, а затем запишет при помощи дробей результаты.

gladtolearn.ru

Объясните, как записать целое через дробь.

Вспомните квадрат и то, как мы делили его на 4 части. Квадрат — это целое, мы можем записать его как 1. Но как записать в виде дроби: что в числителе, что в знаменателе? Если мы делили квадрат на 4 части, то целый квадрат, это 4/4. Если мы делили квадрат на 8 частей, то целый квадрат это 8/8. Но это все равно квадрат, т.е. 1. И 4/4, и 8/8 — это единица, целое!

Умножение дробей

Умножать дробь на число — элементарно! \( \displaystyle  4\cdot \frac{2}{3}\ \) — вот пример, это произведение четырех и \( \displaystyle  2/3\), не путай с \( \displaystyle  4\frac{2}{3}\) — это четыре целых, две третьих!!! Ну, так вот, \( \displaystyle  4\cdot \frac{2}{3}\ =\frac{4\cdot 2}{3}=\frac{8}{3}=2\frac{2}{3}\).

Умножение смешанной дроби на число: \( \displaystyle  4\cdot 2\frac{2}{5}\) . Умножаешь и целую, и дробную части на \( \displaystyle  4\). Вот как это выглядит: \( \displaystyle  4\cdot 3\frac{2}{5}=12\frac{8}{5}=13\frac{3}{5}\).

Все сложнее при умножении дроби на дробь. 

Алгоритм умножения дроби на дробь

1. Если дробь смешанная, привести ее к виду обыкновенной неправильной дроби;
2. Перемножить числители дробей, перемножить знаменатели дробей;
3. Записать результат умножения числителей в числитель, а знаменателей, в знаменатель.

Вот как все делается: \( \displaystyle  3\frac{2}{5}\cdot 2\frac{1}{3}=\frac{17}{5}\cdot \frac{7}{3}=\frac{119}{15}=7\frac{14}{15}\).

Умножение десятичных дробей на число или на десятичную дробь делается просто в столбик, и без запятых. Главное не забыть что?

Правильно, после умножения поставить запятую, отсчитав справа столько знаков, сколько было в сумме у двух множителей до умножения.

Дроби — коротко о главном

Определения:

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.

Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.

Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle  \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).

Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).

Основное свойство дроби: 

Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).

Действия с дробями:

Сложение/вычитание дробей

• две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
• две обыкновенные дроби с разными знаменателями:
  • приводим дроби к наименьшему общему знаменателю;
  • складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
  • сокращаем полученную дробь
• две смешанные дроби с разными знаменателями:
  • приводим дробные части этих чисел к наименьшему общему знаменателю;
  • по-отдельности складываем/вычитаем целые части и дробные части;
  • если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
  • сокращаем полученную дробь.

Умножение дробей

• умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
• умножение двух обыкновенных дробей:
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь
• умножение двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь;
  • если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

• деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
• деление натурального числа на дробь: число умножаем на дробь обратную данной
• деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
• деление двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).

Приведение дробей к наименьшему общему знаменателю

• найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
• разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
• умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).

Преобразования неправильной дроби в смешанную дробь

• поделите числитель дроби на ее знаменатель;
• остаток от деления запишите в числитель, знаменатель оставьте прежним;
• результат от деления запишите в качестве целой части.

Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).

Сравнение дробей:

• две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
• две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
• две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Обучение дробям в школе AMAkids

В Академии развития детского интеллекта AMAkids проводится обучение математике в режиме онлайн для детей от шести лет. В штате образовательной организации работают квалифицированные преподаватели с большим опытом, которые могут найти индивидуальный подход к каждому ребенку. Занятия проводятся на специальной интерактивной платформе с применением электронного пособия и игровых тренажеров. Педагоги доносят материал не в форме стандартных лекций, а в процессе увлекательной игры, руководствуясь авторской методикой.

Математика онлайн от Академии AMAkids состоит из нескольких блоков: арифметика, геометрия, основы программирования и финансовой грамотности. На занятиях по арифметики дети изучают меры величин, знакомятся с понятиями целых чисел и обыкновенных дробей, учатся выполнять простые числовые операции. На уроках геометрии учащиеся знакомятся с основными геометрическими фигурами и их характерными особенностями, исследуют понятия площади и периметра, симметрии и асимметрии.

Финансовая грамотность включает в себя изучение финансовой безопасности, понятий цены и стоимости, знакомятся с историей валютной системы. Ученики узнают о том, как совершать покупки правильно и с максимальной пользой. На основах программирования дети узнают об алгоритмах и множествах. Дети решают логические задачи и примеры разного уровня сложности, выполняют задания на развитие памяти и произвольного внимания.

Обыкновенные дроби сложение вычитание

Правила сложения

Начнем с дробей, у которых одинаковые знаменатели, это самое простое вычисление – высчитывается сумма только числителей – тех чисел, которые находятся над черточкой.

Например:

Можно записать и так:

Немного сложней выполнить действие сложения, если знаменатели разные. В этом случае необходимо сначала:

Пример:

Далее:

Затем, каждую часть дроби, знаменатель и числитель, нужно умножить на свой множитель, который мы определили:

Далее производим сложение дробей:

Правила вычитания

Действие производится аналогичным образом, если у дроби знаменатели одинаковые, необходимо найти разность числителей.

Если у дроби знаменатели разные, Так же, как и при сложении, находим наименьшее кратное число.