Алгебра

Свойства арифметического квадратного корня

Для упрощения некоторых выражений необходимо использовать особые правила работы с корнями. Сформулируем первое из них:

Математически это правило записывается так:

Например:

Тождество работает для любого количества множителей, а также в обратную сторону:

Однако следующее преобразование недопустимо:

Дело в том, что под знаком радикала не может быть отрицательное число! Слева под двумя радикалами стоят отрицательные числа, а справа под корнем находится уже положительная величина (– 2)•(– 32) = 64. В результате выражение слева не имеет смысл, а справа – имеет, поэтому знака равенства между ними быть не может.

Докажем это правило. Для этого возведем во вторую степень выражение

Получили, что по определению корня можно записать:

Следующее свойство касается дробей:

Символически это выглядит так:

Приведем примеры использования этого свойства:

Теперь докажем это правило. Можно записать, что

Значит, по определению верно равенство

Третье правило помогает извлекать корень из числа, возведенного в степень:

где а –действительное число (в том числе и отрицательное), а k – натуральное число.

Это тождество помогает выполнить следующие действия:

Стоит обратить внимание, что в последнем случае под корнем НЕ стоит отрицательное число, так как на самом деле (– 2)10 – это положительное число. Вообще при возведении любого числа в четную степень получается неотрицательное число

Для доказательства этого факта используем то, что

Зная это, можно выполнить преобразования:

Фактическая функция

Графическое представление функции квадратного корня.

Отображение является биекцией из ₊ на ₊ , обратное отмечено . Эта функция называется функцией извлечения квадратного корня . Геометрически мы можем сказать, что квадратный корень из площади квадрата в евклидовой плоскости — это длина одной из его сторон.
Икс↦Икс2{\ Displaystyle х \ mapsto х ^ {2}}Икс↦Икс{\ Displaystyle х \ mapsto {\ sqrt {x}}}

Предупреждение: площадь выражается в универсальной системе в квадратных метрах, а длина — в метрах. Извлекая квадратный корень из количества, выраженного в квадратных метрах, мы получаем количество, выраженное в метрах. Физики придают особое значение анализу единиц; этот аспект стирается в математике. Действительные числа — это безразмерные константы, а квадратный корень из положительного действительного числа — это положительное действительное число.

Функция квадратного корня проверяет следующие элементарные свойства, действительные для всех положительных действительных чисел x и y  :

Иксзнак равноИкс12{\ displaystyle {\ sqrt {x}} = x ^ {\ frac {1} {2}}}

Икс×узнак равноИкс×у{\ displaystyle {\ sqrt {x \ times y}} = {\ sqrt {x}} \ times {\ sqrt {y}}}

Иксузнак равноИксу{\ displaystyle {\ sqrt {\ frac {x} {y}}} = {\ frac {\ sqrt {x}} {\ sqrt {y}}}}(при условии y > 0 )

Икс2знак равно|Икс|{\ displaystyle {\ sqrt {x ^ {2}}} = | x |}.

• Оно строго возрастает , как обратное возрастающей биекции на ℝ ₊ .
• Она 12-Höldérienne, следовательно, равномерно непрерывный .
• Он дифференцируем по любому строго положительному вещественному x , но не дифференцируем по x = 0 . В этой точке репрезентативная кривая допускает вертикальную половину касательной . Его производная функция определяется выражением:

  ddИксИксзнак равно12Икс{\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} {\ sqrt {x}} = {1 \ более 2 {\ sqrt {x}}}}.

• Он имеет класс C ∞ на ℝ ₊ *:∀нет∈НЕТdнетdИкснетИксзнак равно(-1)нет+1(2нет)!нет!22нет(2нет-1)1Икснет-12.{\ displaystyle \ forall n \ in \ mathbb {N} \ quad {\ frac {\ mathrm {d} ^ {n}} {\ mathrm {d} x ^ {n}}} {\ sqrt {x}} = {(-1)} ^ {n + 1} {(2n)! \ over n! 2 ^ {2n} (2n-1)} {\ frac {1} {x ^ {n-1/2}}}.}
• Его развитие в ряд Тейлора в точке 1, следовательно, для любого действительного числа h такого, что | h | ≤ 1:1-часзнак равно1-∑нетзнак равно1∞внетчаснет с участием внетзнак равно(2нет)!(нет!)222нет(2нет-1)>,{\ displaystyle {\ sqrt {1-h}} = 1- \ sum _ {n = 1} ^ {\ infty} a_ {n} h ^ {n} {\ text {with}} a_ {n} = { (2n)! \ over (n!) ^ {2} 2 ^ {2n} (2n-1)}> 0,}с нормальной сходимостью на (см. ). Коэффициенты выражаются как частные от каталонских чисел по степеням двойки  :внетзнак равноПРОТИВнет-122нет-1.{\ displaystyle a_ {n} = {\ frac {C_ {n-1}} {2 ^ {2n-1}}}.}Первые значенияв1знак равно12,в2знак равно18,в3знак равно116,в4знак равно5128.{\ displaystyle a_ {1} = {\ frac {1} {2}}, a_ {2} = {\ frac {1} {8}}, a_ {3} = {\ frac {1} {16}} , a_ {4} = {\ frac {5} {128}}.}

Слайд 11 Извлечение квадратного корня столбикомЭтот способ позволяет найти приближённое

значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234,567 можно представить, как 03 12 34, 56 70. В отличие от деления снос производится такими группами по 2 цифры.1. Записать число N (в примере — 69696) на листке.2.Найти a, квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая не равная нулю), а квадрат a+1 больше группы старших разрядов числа. Записать найденное a справа от N (это очередная цифра искомого корня). (На первом шаге примера a =2 =2 2=46).3.Записать квадрат a под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа a и записать результат вычитания под ними.

.

.

2

2

2

2

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.

Двигаемся дальше \( \displaystyle x=1\); \( \displaystyle {{1}^{2}}=1\) – меньше трех, тоже отметаем.

А что если \( \displaystyle x=2\)? 

Проверим: \( \displaystyle {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( \displaystyle 1\) и \( \displaystyle 2\), а также между \( \displaystyle -2\) и \( \displaystyle -1\).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции \( \displaystyle y={{x}^{2}}\) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из \( \displaystyle 3\), делов-то!

Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568\ldots \) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.

Функция квадратного корня

Каждому числу соответствует не более чем 1 арифметический квадратный корень. Поэтому формула

задает функцию. Исследуем ее.

Так как под знаком радикала может находиться лишь неотрицательное число, то областью определения корня является множество всех неотрицательных чисел. Такова же и область допустимых значений.

Построим график квадратного корня по точкам. Для этого вычислим ее значения в нескольких точках (указана точность до 0,1):

График функции квадратного корня будет выглядеть так:

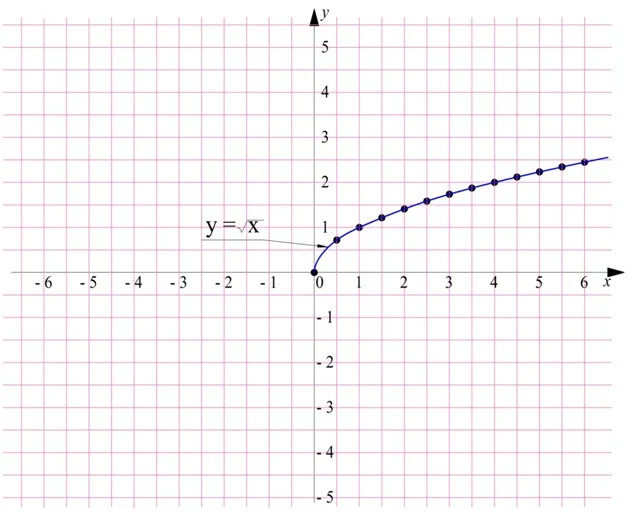
Отметим, что полученная линия чем-то напоминает обычную параболу функции у = х2, которую «положили набок», то есть повернули против часовой стрелки на 90°, а после убрали одну из ветвей:

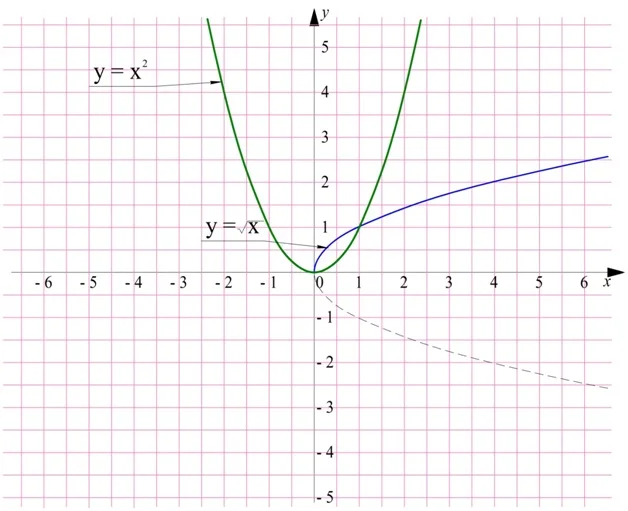
И это не случайность. Дело в том, что две эти функции являются обратными друг другу. Действительно, пусть с помощью графика параболы мы хотим найти значение величины а2. Стрелки показывают последовательность действий:

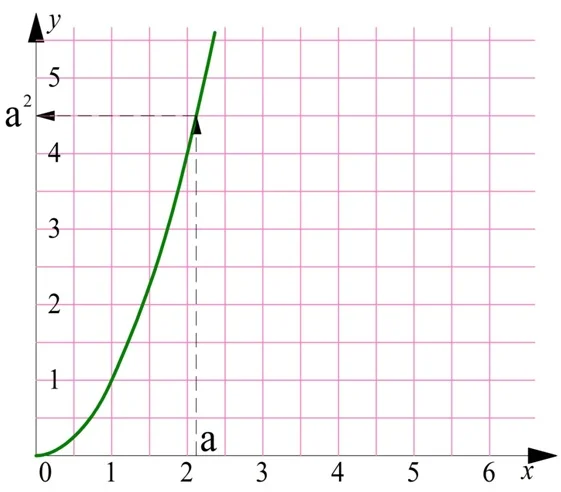
Мы должны найти а на оси Ох, построить от найденной точки вертикальную линию до пересечения с графиком, а потом провести горизонтальную линию. Но если нам надо вычислить корень из положительного числа b, то мы должны действовать в обратном порядке: найти b на вертикальной оси, провести горизонтальную линию до пересечения с параболой, и потом опустить перпендикуляр на горизонтальную ось:

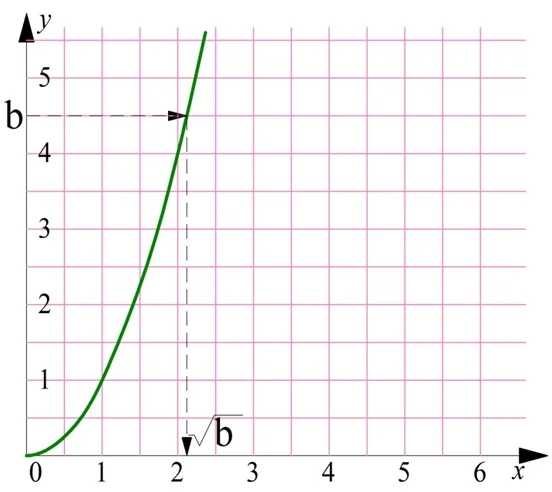
Получается, для вычисления обеих функций можно использовать один график! Но, так как традиционно аргумент функции обозначают буквой х, а саму функцию как у, а также ось Ох располагают горизонтально, то для получения графика обратной функции надо буквально повернуть график основной функции так, чтобы оси Ох и Оу поменялись местами:

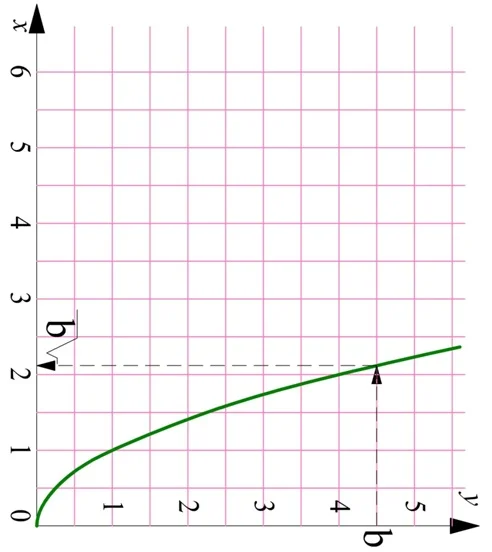
Действительно, в результате поворота получили уже знакомый график функции корня из х. Осталось лишь правильно переименовать оси и повернуть цифры в привычное положение.

Взаимное расположение этих графиков можно описать и иначе. Они симметричны относительно прямой линии, которую задает график у = х. Ведь если точка имеет координаты (а; b) принадлежит параболе у = х2, то, по определению корня, точка с обратными координатами (b; а) должна лежать на графике корня. Однако две такие точки будут симметричны относительно линии у = х:

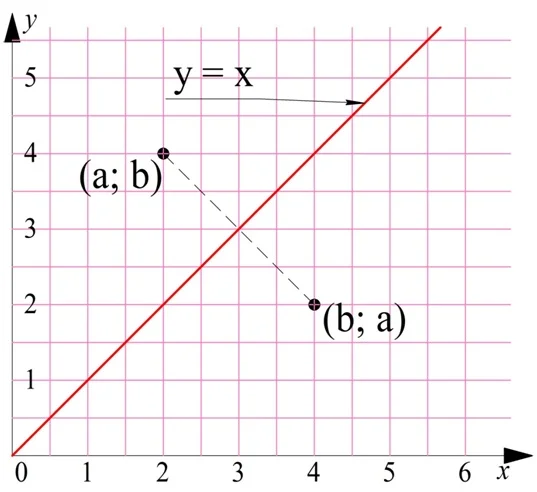
Соответственно, симметричны относительно этой прямой и графики обратных функций:

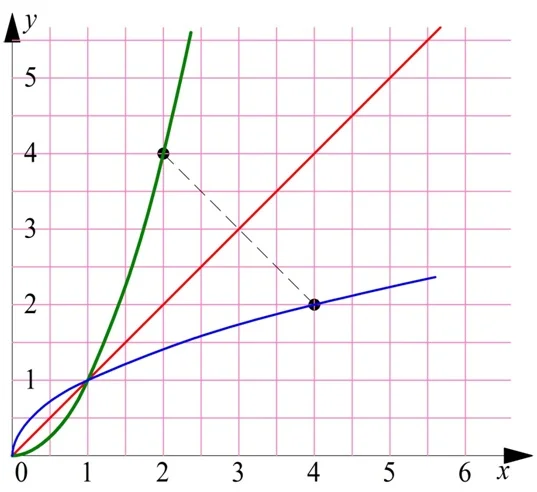
Исключительно для большей наглядности (чтобы была очевидна симметрия, о которой идет речь), повернем эту картинку на 45°:

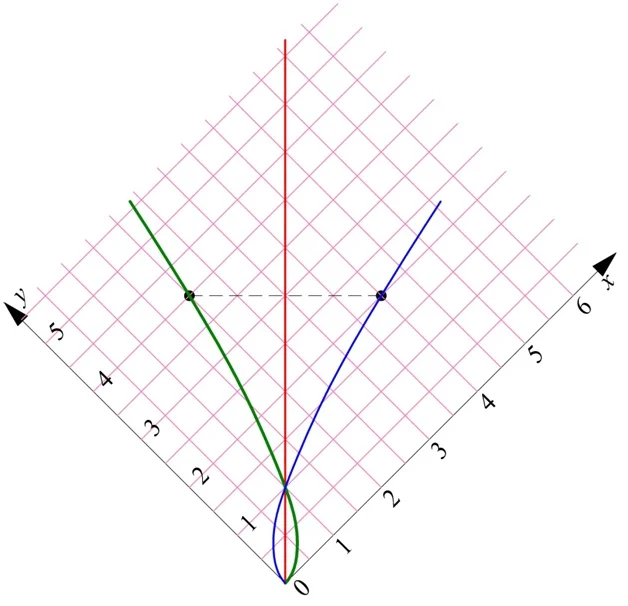
Сравнение корней

Зачем нам учиться сравнивать числа, содержащие квадратный корень?

Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)

Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!

Например, определи, что больше: \( \displaystyle   3\sqrt{7}\) или \( \displaystyle   2\sqrt{17}\)?

Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?

Тогда вперед:

Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!

Т.е. если \( \displaystyle 68>63\), значит, \( \displaystyle   \sqrt{68}>\sqrt{63}\).

Отсюда твердо делаем вывод, что \( \displaystyle   3\sqrt{7}<2\sqrt{17}\).

Геометрическое построение квадратного корня

AO = 1, OB = a, OH = √ a

Следующее геометрическое построение выполняется с помощью линейки и циркуля и позволяет из отрезка OB длины a и отрезка длины 1 построить отрезок длины √ a  :

• Постройте отрезок длины 1 + a, содержащий точку O с AO = 1.
• Построить окружность C в диаметре .
• Постройте прямую d, перпендикулярную (OB) и проходящую через O.
• Назовите H точку пересечения окружности c и прямой d .

Отрезок имеет длину √ a .

Доказательство состоит в том, чтобы что треугольники OAH и OHB подобны , из чего мы заключаем, что OH 2 = AO × OB = a , и, следовательно, OH = √ a .

Эта конструкция имеет важное значение при изучении конструктивных чисел .

Вычисление квадратного корня

Ранее для выполнения арифметических операций мы использовали метод «столбика». А как производить вычисление квадратного корня? Существует несколько приемов, мы рассмотрим простейший из них.

Очевидно, что чем больше число, тем больше и его квадрат. Например, 5 > 4, поэтому и 52> 42. Значит, справедливо и обратное утверждение: чем больше число, тем больше и его квадратный корень.

Убедиться в этом можно и с помощью графика функции у = х2. Будем отмечать на нем числа и их квадратные корни:

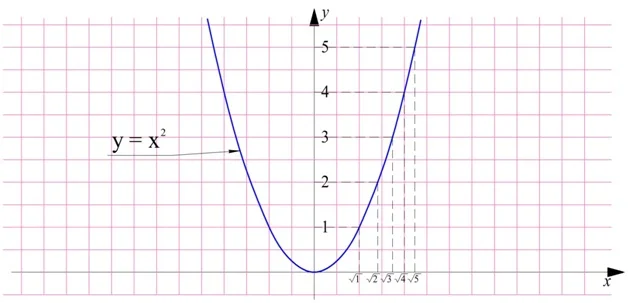
Видно, что чем выше на оси Оу располагается число, тем правее на оси Ох находится его квадратный корень.

Зная это свойство, легко оценить значение корня из любого числа. Продемонстрируем это на примере вычисления значение корня из 2. Нам известно, что

1 < 2 < 4

Значит, можно записать следующие неравенства:

Нам удалось определить, что корень из двух находится между единицей и двойкой, то есть

Теперь определим первую цифру после запятой для корня из двух. Будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3 и т. д, до тех пор пока не получим выражение, большее 2:

1,12 = 1,21

1,22 = 1,44

1,32 = 1,69

1,42 = 1,96

1,52 = 2,25

Теперь мы можем записать неравенства:

Получается, что корень имеет значение, находящееся между 1,4 и 1,5, то есть

Попытаемся определить ещё одну цифру после запятой:

1,412 = 1,999396

1,422 = 2,002225

Отсюда следует, что:

Продолжая подобные вычисления, можно вычислить любое количество знаков после запятой:

Конечно, на практике все вычисления выполняются компьютером, а не вручную. Однако программисты стремятся написать программы так, чтобы они работали как можно быстрее, то есть получали результат, выполняя меньшее количество вычислений. Поэтому на практике чаще используется метод бисекции (деления надвое), который отличается большей эффективностью. Для начала нужно найти очевидную оценку корня, например:

Получили, что корень из 2 находится между 1 и 2. Теперь найдем среднее арифметическое этих двух значений:

(1 + 2)/2 = 1,5

Возведем среднее арифметическое в квадрат:

1,52 = 2,25

Теперь мы можем записать неравенство

То есть искомое нами значение находится между 1 и 1,5. Снова найдем среднее этих двух оценок и возведем его в квадрат:

(1 + 1,5)/2 = 1,25

1,252 = 1,5625

Зная это, можем записать:

На каждом следующем шаге вычислений мы будем всё точнее определять оценки корня, при этом вычислений мы делаем не очень много.

Периодически могут встречаться задания, в которых надо грубо оценить значение квадратного корня.

Пример. Сколько целых чисел на координатной прямой располагается между

Решение: Ближайшие к числу 60 полные квадраты – это 64 и 49, поэтому можно записать:

Также можно оценить и корень из 140:

Получаем, что между корнями располагается четыре числа: 8, 9, 10 и 11:

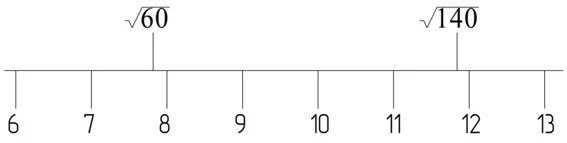
Ответ: 4

Извлечение корней

Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.

Для этого необходимо знать, по меньшей мере, квадраты чисел от \( \displaystyle 1\) до \( \displaystyle 20\), а также уметь их распознавать.

То есть, тебе необходимо знать, что \( \displaystyle 15\) в квадрате равно \( \displaystyle 225\), а также, наоборот, что \( \displaystyle 225\) – это \( \displaystyle 15\) в квадрате.

Первое время в извлечении корня тебе поможет эта таблица.

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.

Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:

• \( \sqrt{0}=?\);
• \( \sqrt{64}=?\);
• \( \sqrt{121}=?\);
• \( \sqrt{289}=?\);

Ответы:

• \( \displaystyle 0\);
• \( \displaystyle 8\);
• \( \displaystyle 11\);
• \( \displaystyle 17\);

Ну как, получилось? Теперь давай посмотрим такие примеры:

• \( \sqrt{0,0196}=?\);
• \( \sqrt{0,0961}=?\);
• \( \sqrt{0,0144}=?\).

Ответы:

• \( \displaystyle 0,14\);
• \( \displaystyle 0,31\);
• \( \displaystyle 0,12\);

Что такое арифметический квадратный корень

А почему же число  \( a\) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен \( \sqrt{-9}\)?

Так-так, попробуем подобрать. Может, три?

Проверим: \( {{3}^{2}}=9\), а не \( -9\).

Может, \( \left( -3 \right)\)? 

Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

 Ведь в определении сказано, что «квадратным корнем из числа\( a\)называется такое неотрицательное число, квадрат которого равен\( a\)».

Но подождите!  В самом начале мы разбирали пример \( {{x}^{2}}=4\) и один из ответов был отрицательным числом! 

 Мы подбирали числа, которые можно возвести в квадрат и получить при этом \( \displaystyle 4\). Ответом были \( \displaystyle 2\) и \( \displaystyle -2\)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, \( \displaystyle {{x}^{2}}=4\) (квадратное уравнение) не равносильно выражению \( x=\sqrt{4}\) (арифмитический квадратный корень).

Из \( {{x}^{2}}=4\) следует, что

\( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2\); \( {{x}_{2}}=-2\)

(не помнишь почему так? Почитай тему «Модуль числа»!)

А из \( x=\sqrt{4}\) следует, что \( x=2\).

Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как \( 2\), так и \( x=-2\).

Внесение под знак корня

Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!

Это совсем легко!

Допустим, у нас записано число \( \displaystyle   3\sqrt{5}\)

Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из \( \displaystyle   9\)!

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.

Реши самостоятельно вот этот пример — \( \displaystyle   4\sqrt{6}-2\sqrt{3}\cdot \sqrt{8}\)

Справился? Давай смотреть, что у тебя должно получиться:

Примечания и ссылки

(fr) Эта статья частично или полностью взята из английской статьи в Википедии под названием .

1. Mistral Collection, Mathematics 3 th , 1985, p.  20
2. Для элементарного доказательства см., Например, .
3. Для демонстрации см., Например, .
4. В решении уравнения третьей степени , метод Кардано является прикладным формально и дает реальные результаты, если один принимает ввести в некоторых случаях «мнимые» квадратные корни отрицательных чисел. Для получения дополнительной информации см. , а также .
5. Люкс A010503 из OEIS . 
6. Однако в статье «  Риманова поверхность  » можно найти способ обойти эту трудность.

Свойства арифметического квадратного корня

Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:

• умножение;
• деление;
• возведение в степень.

Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:

СВОЙСТВО	ПРИМЕР
Корень произведения равен произведению корней:  \( \displaystyle \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}\)	\( \displaystyle \sqrt{64\cdot 9}=\sqrt{64}\cdot \sqrt{9}=8\cdot 3=24\)
Корень из дроби — это корень из числителя и корень из знаменателя: \( \displaystyle \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\), если \( \displaystyle a\ge 0\ ,\ b > 0\)	\( \displaystyle \sqrt{\frac{64}{9}}=\frac{\sqrt{64}}{\sqrt{9}}=\frac{8}{3}=2\frac{2}{3}\)
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: \( \displaystyle {{\left( \sqrt{a} \right)}^{n}}={{\left( \sqrt{{{a}^{n}}} \right)}^{{}}}\), при \( \displaystyle a\ge 0\)	\( \displaystyle {{\left( \sqrt{2} \right)}^{4}}=\sqrt{{{2}^{4}}}=\sqrt{16}=4\)

Преобразование выражений с квадратными корнями

Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:

Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:

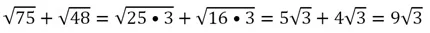
Обратное действие называют внесением множителя под знак корня:

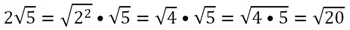
Пример. Какое число больше

Решение. Внесем множитель под знак корня:

Из двух корней больше тот, у которого больше подкоренное выражение, поэтому

Из этого следует, что

Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:

Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:

Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула :

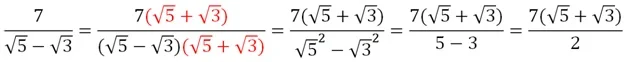
Рассмотрим несколько задач.

Пример. Найдите наибольшее значение выражения

Решение. По формуле разности квадратов можно записать:

Зная это, заменим знаменатель дроби:

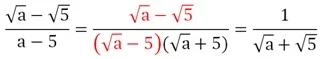
Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять

Пример. Упростите выражение

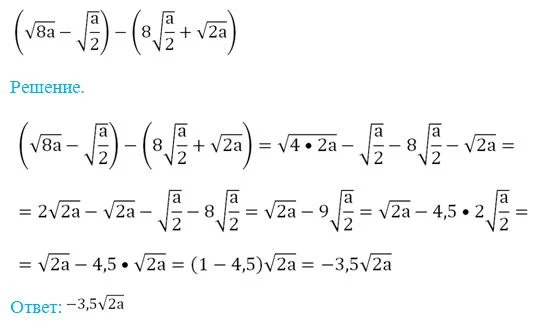
Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида

называют двойным радикалом.

Существует формула двойного радикала, с помощью которой его можно иногда упростить:

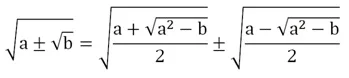
Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя (х ± у)2 = х2 ± 2ху + у2:

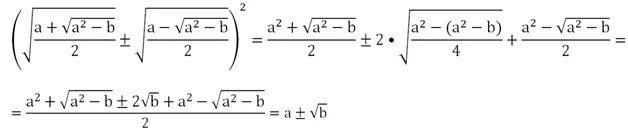
Принципиально важно, что величина а2 – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере

Пусть надо освободиться от внешнего радикала в выражении

Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:

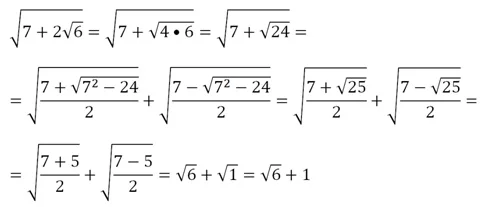
Заметим, что формула двойного радикала полезна в том случае, если выражение а2 – b является полным квадратом.