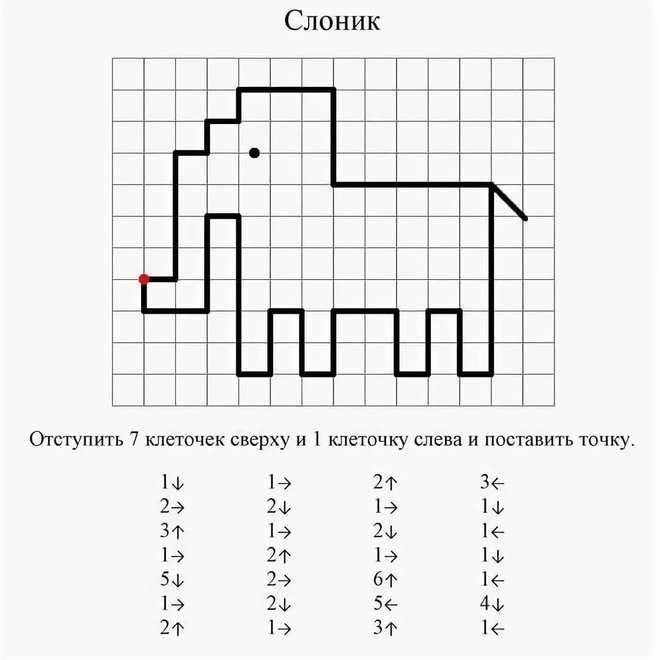
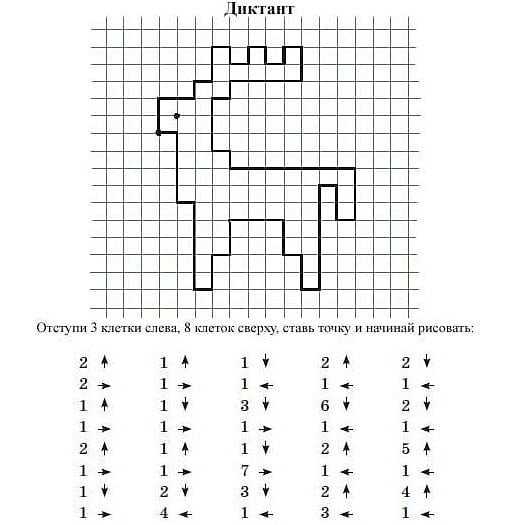
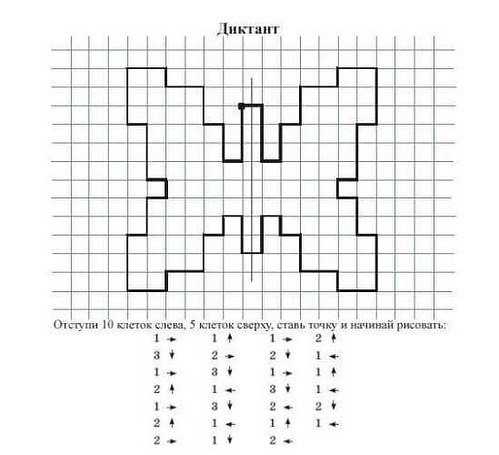
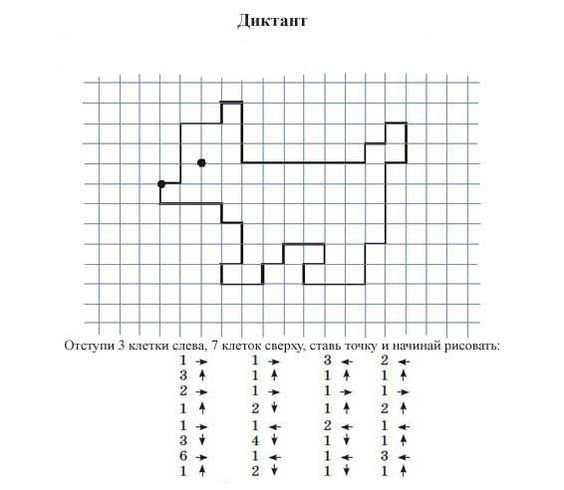
Графический диктант рак
Рак
- 6 вверх
- 2 по диагонали вправо вверх
- 7 вниз
- 1 вправо
- 7 вверх
- 1 вправо
- 8 вниз
- 3 вправо
- 6 вверх
- 1 по диагонали вправо вверх
- 1 влево
- 2 вверх
- 2 влево
- 2 вверх
- 1 влево
- 1 вниз
- 2 вправо
- 2 вниз
- 2 вправо
- 1 вниз
- 1 по диагонали вправо вверх
- 1 по диагонали вправо вниз
- 1 вверх
- 2 вправо
- 2 вверх
- 2 вправо
- 1 вверх
- 1 влево
- 2 вниз
- 2 влево
- 2 вниз
- 1 влево
- 1 по дагонали вправо вниз
- 6 вниз
- 3 вправо
- 8 вверх
- 1 вправо
- 7 вниз
- 1 вправо
- 7 вверх
- 2 по диагонали вправо вниз
- 6 вниз
- 1 влево
- 1 вниз
- 1 влево
- 1 вниз
- 6 влево
- 2 вниз
- 2 вправо
- 1 вниз
- 2 по диагонали вправо вниз
- 1 влево
- 2 по диагонали влево вверх
- 1 влево
- 2 вниз
- 2 вправо
- 1 вниз
- 2 по диагонали вправо вниз
- 1 влево
- 2 по диагонали влево вверх
- 1 влево
- 2 вниз
- 2 вправо
- 4 вниз
- 1 влево
- 3 вверх
- 1 влево
- 3 вниз
- 1 по диагонали вправо вниз
- 4 влево
- 1 по диагонали вправо вверх
- 3 вверх
- 1 влево
- 3 вниз
- 1 влево
- 4 вверх
- 2 вправо
- 2 вверх
- 1 влево
- 2 по диагонали влево вниз
- 1 влево
- 2 по диагонали вправо вверх
- 1 вверх
- 2 вправо
- 2 вверх
- 1 влево
- 1 по диагонали влево вниз
- 1 влево
- 2 по диагонали вправо вверх
- 1 вверх
- 2 вправо
- 2 вверх
- 6 влево
- 1 вверх
- 1 влево
- 1 вверх
- 1 влево
Дубовый лист
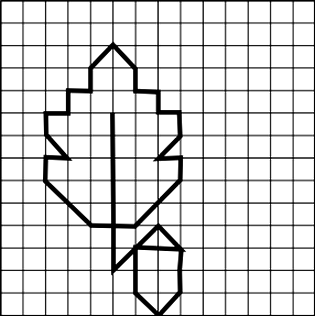
Начальная точка – 5 клеток вниз, 5 клеток вправо.
- 5 клеток вниз
- 1 клетка влево
- 2 клетки влево вверх наискосок
- 1 клетка вверх
- 1 клетка вправо
- 1 клетка влево вверх наискосок
- 1 клетка вверх
- 1 клетка вправо
- 1 клетка вверх
- 1 клетка вправо
- 1 клетка вверх
- 1 клетка вправо вверх наискосок
- 1 клетка вправо вниз наискосок
- 1 клетка вниз
- 1 клетка вправо
- 1 клетка вниз
- 1 клетка вправо
- 1 клетка вниз
- 1 клетка влево вниз наискосок
- 1 клетка вправо
- 1 клетка вниз
- 2 клетки влево вниз наискосок
- 1 клетка влево
- 2 клетки вниз
- 2 клетки вправо вверх наискосок
- 1 клетка вправо вниз наискосок
- 2 клетки влево
- 2 клетки вниз
- 1 клетка вправо вниз наискосок
- 1 клетка вправо вверх наискосок
- 2 клетки вверх.
Польза от диктанта
Несомненно, полезность такого вида диктанта неоспорима. Над разработкой механизмов его воздействия работала группа авторов-педагогов. Один из них – Шевелёв Константин
Валерьевич – разработал целый курс, содержащий поэтапные занятия с детьми дошкольного возраста, а также учащимися первых классов.
Благодаря этим специальным тетрадям у детей появляется возможность развить и улучшить работу памяти, задействовать воображение, развить мелкую моторику рук, внимание, улучшить координацию движений, орфографическую зоркость и грамотность, расширить запас слов. Одновременно с этим повышается самооценка ребёнка
- Расширение кругозора также является одной из основных задач этого метода.
- Все картинки подбираются, исходя из возрастных особенностей малышей. Но это только первое время.
- Далее необходимо изображать уже рисунки, с которыми дети не знакомы.
- В дополнение к изображению, например, какого-нибудь животного можно рассказать о нём и показать фотографию.
Практические задания для закрепления знаний о отрезках
1. Найдите длину отрезка, заданного точками А(3,5) и В(8,9).
2. Заданы точки А(2,4) и В(7,2). Определите, находится ли точка С(3,3) на отрезке АВ.
3. Найдите координаты точки D, которая делит отрезок АВ в отношении 3:4, если А(2,5), а В(8,11).
4. Известны координаты точек А(3,-5), В(7,1) и С(9,-4). Определите, являются ли точки А, В, С вершинами прямоугольника.
5. Найдите значение коэффициента, определяющего уравнение прямой, проходящей через точки А(2,3) и В(6,9).
- 6. Постройте на координатной плоскости отрезок, заданный точками А(-2,5) и В(6,-3).
- 7. Задана точка А(4,1) и длина отрезка ВС. Найдите координаты точек В и С, если точка В лежит на оси абсцисс, а точка С – на оси ординат.
- 8. Известны координаты точек А(0,1) и В(3,4). Определите координаты точки С, симметричной А относительно В.
9. Вам даны координаты точек А(2,4), В(7,2) и С(5,9). Определите, какая из этих точек находится дальше от точки А: В или С?
Номер заданияУсловиеОтвет
| 1 | Найдите длину отрезка, заданного точками А(3,5) и В(8,9). | 5 |
| 2 | Заданы точки А(2,4) и В(7,2). Определите, находится ли точка С(3,3) на отрезке АВ. | да |
| 3 | Найдите координаты точки D, которая делит отрезок АВ в отношении 3:4, если А(2,5), а В(8,11). | D(5.2;7.6) |
| 4 | Известны координаты точек А(3,-5), В(7,1) и С(9,-4). Определите, являются ли точки А, В, С вершинами прямоугольника. | нет |
| 5 | Найдите значение коэффициента, определяющего уравнение прямой, проходящей через точки А(2,3) и В(6,9). | 1.5 |
Что такое отрезок в математике 2 класса?
Отрезок — это часть прямой, ограниченная двумя точками, называемыми концами отрезка. В математике 2 класса изучаются простейшие свойства отрезков, такие как длина и нахождение середины отрезка.
Как измеряется длина отрезка в математике 2 класса?
Для измерения длины отрезка в математике 2 класса используется единица измерения — сантиметр. Длина отрезка определяется как расстояние между его концами, и измеряется в сантиметрах.
Что такое середина отрезка в математике 2 класса?
Середина отрезка — это точка находящаяся на равном расстоянии от его концов. В математике 2 класса середина отрезка находится путем деления его на две равные половины.
Как находить середину отрезка в математике 2 класса?
Чтобы найти середину отрезка в математике 2 класса, нужно его разделить на две равные части. Для этого можно использовать линейку или компас. Сначала на линейке или с помощью компаса находим середину отрезка, отмечая ее точку на прямой. Затем с помощью линейки проводим прямую, проходящую через середину отрезка и перпендикулярную к прямой, на которой находится данный отрезок.
В чем отличие отрезка от открытого интервала?
Отрезок — это часть прямой, ограниченная двумя точками, включая эти точки. Открытый интервал — это часть прямой, не включающая свои конечные точки. Таким образом, отличие заключается в том, что отрезок включает свои конечные точки, а открытый интервал их не включает.
Можно ли нарисовать отрезок с нулевой длиной?
Не существует отрезка с нулевой длиной, так как отрезок — это часть прямой, ограниченная двумя точками, и если его длина равна нулю, то это означает, что две его конечные точки совпадают, и это уже не является отрезком.
Для чего нужно изучать отрезок в математике 2 класса?
Изучение отрезка в математике 2 класса необходимо для формирования базовых математических понятий и навыков, таких как измерение длины и построение геометрических фигур
Знание свойств отрезков важно и в дальнейшем обучении математике
Презентация на тему: » «Графические диктанты» ( рисование по клеточкам).» — Транскрипт:
1
«Графические диктанты» ( рисование по клеточкам)
2
Рисование по клеточкам- очень увлекательное и полезное занятие для детей. Это игровой способ развития у ребенка пространственного воображения, мелкой моторики пальцев, координации движений, усидчивости.
3
Графические диктанты с успехом могут применяться для детей разного возраста.
4
Графические диктанты хорошо помогают развивать у детей орфографическую зоркость, неусидчивость и рассеянность.
5
Регулярные занятия с графическими диктантами развивают у ребенка произвольное внимание, пространственное воображение, мелкую моторику пальцев рук, координацию движений, усидчивость
6
Выполняя задания в графических диктантах ребенок учится ориентироваться в тетради, знакомится с разными способами изображения предметов.
7
Как работать с графическими диктантами:
8
Графический диктант можно выполнять в двух вариантах: 1.Ребенку предлагают образец геометрического рисунка и просят его повторить точно так же. 2. Взрослый диктует последовательность действий с указанием числа клеточек и их направлений( влево, вправо, вверх, вниз), ребенок выполняет работу на слух.
9
Графические диктанты дополнены загадками, скороговорками, чистоговорками и пальчиковой гимнастикой. В процессе занятия ребенок отрабатывает правильную, четкую и грамотную речь, развивает мелкую моторику, учится выделять отличительные особенности предметов, пополняет словарный запас.
10
Задания подобраны «от простого к сложному».
11
Для занятий необходима тетрадь в клетку, простой карандаш и ластик, чтобы ребенок мог всегда исправить неправильную линию.
13
Во время занятий очень важен настрой ребенка и доброжелательное отношение взрослого..
14
Важно помнить, что занятие для ребенка -не экзамен, а всего лишь игра
15
Необходимо помогать ребенку, следить за тем, чтобы он не ошибался. Ведь результат работы всегда должен удовлетворять ребенка, чтобы ему вновь и вновь хотелось рисовать по клеткам.
16
Моя задача- помочь ребенку в игровой форме овладеть необходимыми для хорошей учебы навыками.
17
Нельзя ругать ребенка. Если у ребенка что-то не получается, нужно просто объяснить, как надо делать правильно
Важно чаще хвалить ребенка и никогда ни с кем не сравнивать
18
Продолжительность одного занятия с графическими диктантами не должна превышать минут, но если ребенок увлекся не стоит его останавливать и прерывать занятие.
19
Важно обратить внимание на посадку ребенка во время выполнения задания, на то, как он держит карандаш. Если не правильно нужно показать
20
20
Сели прямо, ноги вместе, Под наклон возьмём тетрадь. Левая рука на месте, Правая рука на месте, Можно начинать писать!!!
22
Если ребенок плохо считает необходимо помогать ему отсчитывать клетки в тетради.
23
После этого начинаем работу в тетради и в ней ищем левый- правый края, вер- низ. Кто плохо помнит подписываем : лево- буква «л»; право- буква «п».
25
Когда ребенок нарисует смотрим, что получилось. И радуемся результатом.
26
После работы говорим с детьми, что есть предметы и есть их изображения. Изображения бывают разные: фотографии, рисунки, схематическое изображение. Графический диктант- это схематическое изображение предмета.
27
Говорим с детьми о том, что каждое животное ил предмет имеет свои отличительные особенности, по которым мы можем его узнать. После того, как нарисовали зайца, спрашивала, какие отличительные особенности у этого животного.
28
Наши достижения:
29
Первые работы Ситниковой Наташи
30
«Слоник и домик» Ситниковой Наташи
31
«Зайка и машина» Ситниковой Наташи
32
Работы Чипчагова Сергея Пробный рисунок «ЧЕЛОВЕЧКА» «Человечек»
33
Работы Чипчагова Сергея «Гусеница» «Птичка»
34
Пробные работы Норкина Жени «Человечек»
35
«Собачка» Норкина Жени
36
Работы Норкина Жени «Слоник» «Ключик»
37
Работы Макарова Миши «Плюсик» «Флажок»
38
«Ключик» Храпина Витали
39
РАБОТЫ Животягиной Наташи
40
Работы Животягиной Наташи «Слоник» «Чебурашка»
41
«Пробный узор» Речкаловой Наташи
42
Работы Речкаловой Наташи «Чебурашка»«Домик»
43
«Зайчики» Овчинникова Сергея
44
«Собачка» Барановой Яны
45
Работы Осинцевой Лены
46
«Домик и кораблик» Осинцевой Лены
47
Работы Черняева Славы
48
Рисование по клеткам формирует ловкость руки и твердость глаза, развивает такие навыки, как зрительно-пространственный анализ, зрительно-моторную координацию. А все это — отличная подготовка руки к письму.
49
Рисование по клеткам способствует навыкам счета (необходимо сосчитать число клеток прежде, чем провести линию); закреплению понятий ВВЕРХ, ВНИЗ, СВЕРХУ ВНИЗ, СЛЕВА НАПРАВО и т.п.
50
Спасибо за внимание!
Как определять длину отрезка
Длина отрезка — это расстояние между его конечными точками. Для определения длины отрезка нужно знать координаты его начальной и конечной точек. Если даны координаты точек на плоскости, то можно использовать теорему Пифагора.
Для нахождения длины отрезка через координаты начальной и конечной точек нужно:
- Вычислить разность координат по оси X между конечной и начальной точками
- Вычислить разность координат по оси Y между конечной и начальной точками
- Применить теорему Пифагора, применив найденные значения как катеты
Например, для отрезка с конечными точками A(3,2) и B(6,4) нужно:
- Вычислить разность координат по оси X: 6 — 3 = 3
- Вычислить разность координат по оси Y: 4 — 2 = 2
- Применить теорему Пифагора: √(3² + 2²) ≈ 3.6
Таким образом, длина отрезка AB ≈ 3.6.
Что такое отрезок
Отрезок в математике – это участок прямой линии, ограниченный двумя точками на ней. Отрезок имеет конечную длину и может быть изображен в виде линии, которая соединяет две точки.
Для обозначения отрезка используют две буквы, которые указывают на имена точек, между которыми находится отрезок. Например, отрезок, который соединяет точки А и В, обозначается как AB.
Отрезки могут быть разной длины. Если отрезок имеет одинаковые точки на концах, то такой отрезок называется нулевым и имеет длину 0.
Важно помнить, что отрезок – это часть прямой линии, а не все её полное описание. Хотя отрезок может быть представлен линией, линия может продолжаться бесконечно в обе стороны, в то время как отрезок имеет ограниченную конечную длину и является замкнутой фигурой
Как рисовать отрезок
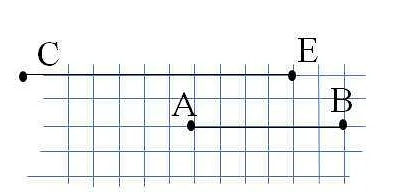
Отрезок — это линия, которая имеет начальную и конечную точку. Его можно нарисовать на листе бумаги.
Для этого необходимо:
- Нанести на лист бумаги две точки с помощью карандаша и линейки, которые будут являться начальной и конечной точкой отрезка.
- С помощью линейки провести прямую линию через эти точки.
Важно помнить, что отрезок должен быть ровной прямой линией, а также длина отрезка должна соответствовать заданным в условии размерам. При рисовании отрезка также важно следить за масштабом
Если отрезок имеет размер 5 см, а вы его нарисуете на листе бумаги в 10 раз увеличенном масштабе, то его длина на листе будет 50 см
При рисовании отрезка также важно следить за масштабом. Если отрезок имеет размер 5 см, а вы его нарисуете на листе бумаги в 10 раз увеличенном масштабе, то его длина на листе будет 50 см
Пример отрезков
| Начальная точка | Конечная точка | Отрезок |
| (2,3) | (4,5) | AB |
| (0,0) | (5,0) | CD |
На картинке выше показаны два примера отрезков с координатами начальной и конечной точки
Очень важно понимать, что каждый отрезок имеет свои размеры и координаты, а также может быть нарисован в разных масштабах
Оценка результатов
Результаты выполнения тренировочного узора не оцениваются. В каждом из последующих узоров оценивается порознь выполнение диктанта и самостоятельное продолжение узора. Оценка производится по следующей шкале:
4 балла – точное воспроизведение узора. (Неровности линии, «дрожащая» линия, «грязь» и т.п. не учитываются и не снижают оценки).3 балла – воспроизведение, содержащее ошибку в одной линии.2 балла – воспроизведение с несколькими ошибками.1 балл – воспроизведение, в котором имеется лишь сходство отдельных элементов с диктовавшимся узором.0 баллов – отсутствие сходства даже в отдельных элементах.
За самостоятельное продолжение узора оценки выставляются по этой же шкале.
Таким образом, за каждый узор ребенок получает по две оценки: одну – за выполнение диктанта, другую – за продолжение узора. Обе они колеблются в пределах от 0 до 4. Итоговая оценка работы под диктовку выводится из трех соответствующих оценок за отдельные узоры путем суммирования максимальной из них с минимальной, оценка, занимающая промежуточное значение или совпадающая с максимальной или минимальной, не учитывается. Полученная оценка может колебаться от 0 до 8 баллов. Аналогично из трех оценок за продолжение узора выводится итоговая оценка. Затем обе оценки суммируются, давая суммарный балл (СБ), который может колебаться в пределах от 0 (если за работу под диктовку и за самостоятельную работу получено по 0 баллов) до 16 (если за оба вида работы получено по 8 баллов).
В дальнейшем анализе используется только итоговый показатель, который интерпретируется следующим образом:
Низкий — 0-3 балла
Ниже среднего 4-6 баллов
Средний — 7-10 баллов
Выше среднего — 11-13 баллов
Высокий — 14-16 баллов
Литература: Истратова О.Н. Справочник психолога начальной школы / О.Н.Истратова, Т.В.Эксакутсто. – Изд. 6-е. – Ростов н/Д: Феникс,2008. – 442 с.
или:
Рисование по клеточкам для начинающих
Рисование по клеточкам можно начинать с простых узоров. Постепенно переходя к более сложным ритмическим рисункам и графическим диктантам.
Для начала можно использовать простое копирование рисунка по клеточкам
На таких заданиях ребенок научится сравнивать и разовьет свое внимание
Но все же, для развития мозга малыша, необходимо использовать более сложные и развивающие задания, нежели простое копирование.
В них активно подключается работа мысли, развивается логика и математическое мышление. Приведу в пример несколько подобных упражнений со страниц своих книг.
Также необходимо помнить и о развитии кругозора малыша.
Поэтому предлагаю малышам открыть для себя мир живой природы, классифицированный по тематическим группам. Ребёнок сможет не только научиться рисовать по клеточкам указанных представителей, но придумывать и добавлять своих. Эти занятия послужат хорошим толчком для развития кругозора и творческих способностей ребенка.
Поэтому с удовольствием делюсь с вами еще очень интересным и развивающим материалом.
В качестве примера поместила одну из первых страничек. Она касается насекомых. В книге также есть странички, посвященные лесным, морским, домашним животным, животным жарких стран, обитателям водоёмов, но и конечно же растениям.
Таким образом, рисование по клеточкам учит ребёнка ориентироваться на плоскости листа, что очень важно при обучении в школе. Кроме того, ребенок развивает:
пространственное мышление;
внимание;
мелкую моторику руки;
приобретает умение соотносить образец и свой рисунок;
учится сравнивать;
находить и исправлять ошибки.
Упражняться в этом увлекательном занятии можно каждый день. Оно принесёт вашему ребенку только пользу.
Барашек
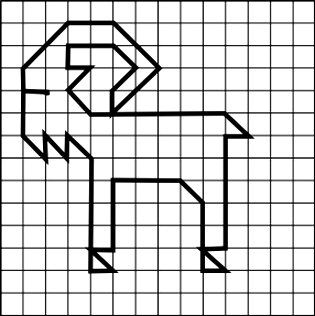
Начальная точка – 5 клеток вниз, 3 клетки вправо.
- 1 клетка влево
- 1 клетка вверх
- 2 клетки вправо вверх по диагонали
- 2 клетка вправо
- 2 клетки вправо вниз по диагонали
- 2 клетки влево вниз по диагонали
- 1 клетка вверх
- 1 клетка вправо вверх по диагонали
- 1 клетка влево вверх по диагонали
- 2 клетки влево
- 1 клетка вниз
- 1 клетка вправо
- 1 клетка влево вниз по диагонали
- 1 клетка вправо вниз по диагонали
- 6 клеток вправо
- 1 клетка вправо вниз по диагонали
- 1 клетка влево
- 5 клеток вниз
- 1 клетка влево
- 1 клетка вправо вниз по диагонали
- 1 клетка влево
- 3 клетки вверх
- 1 клетка влево вверх по диагонали
- 3 клетки влево
- 3 клетки вниз
- 1 клетка влево
- 1 клетка вправо вниз по диагонали
- 1 клетка влево
- 5 клеток вверх
- 1 клетка влево вверх по диагонали
- 1 клетка вниз
- 1 клетка влево вверх по диагонали
- 1 клетка вниз
- 1 клетка влево вверх по диагонали
- 2 клетки вверх.
Задача о количестве отрезков на чертеже 2 класс математика стр 27
Задача формулируется следующим образом: на чертеже дано несколько отрезков, и нужно определить их количество. Отрезки на чертеже обычно обозначаются линиями заданной длины. Ученик должен посчитать число отрезков, не забывая учитывать каждый отрезок только один раз.
Решение задачи требует от ученика концентрации и внимательности. Он должен аккуратно просмотреть чертеж и отметить каждый отрезок. Дети могут использовать стрелки или другие способы, чтобы не пропустить отрезки. Они могут также применять различные методы счета, например, считать отрезки по очереди или использовать числовой ряд.
Задача о количестве отрезков на чертеже является важным шагом в изучении геометрии. После ее решения дети могут приступить к более сложным задачам, связанным с геометрическими фигурами, углами и пересечениями.
Эта задача также помогает детям перенести свои навыки счета на практику, применяя их для анализа и решения различных задач. Она развивает их математическое мышление, логику и способность решать задачи поэтапно.
Таким образом, задача о количестве отрезков на чертеже 2 класс математика стр 27 является не только решением конкретной задачи, но и важным шагом в развитии учеников твердых математических навыков и умений.
Зачем малышам знать и уметь считать треугольники
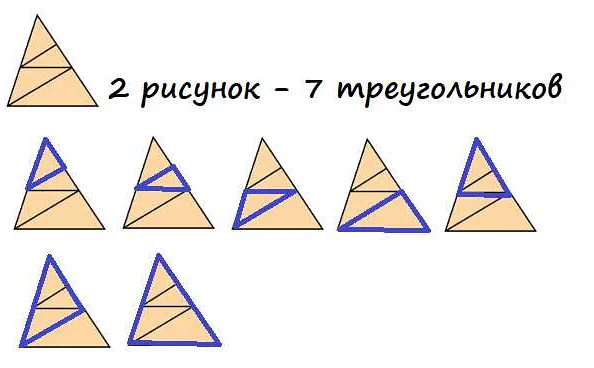
Считать треугольники – это одно из основных математических умений, которые должен освоить каждый ребенок. Нельзя недооценивать значение этого навыка, ведь он не только развивает математическое мышление, но и пригодится в жизни за пределами школьной классной комнаты.
С помощью треугольников малыши изучают пространственную структуру, формы и объемы. Это позволяет им лучше понимать окружающий мир, воспринимать его в трех измерениях и узнавать различные геометрические фигуры. Кроме того, умение считать треугольники помогает развивать в детях воображение и творческие способности.
Знания в области геометрии помогут ребенку решать задачи на ежедневной основе, например, при расчете площади или периметра форм, нахождении геометрических центров и т.д. Кроме того, геометрия важна при проектировании и строительстве, а также в различных технических профессиях.
Таким образом, умение считать треугольники не только помогает развивать интеллектуальные способности ребенка, но и пригодится ему в будущем жизненном пути
Поэтому, важно не забывать о значимости этого простого, но важного математического умения
Почему важно знать количество отрезков на чертеже?
Зная количество отрезков на чертеже, ученик может легче понять структуру и компоненты изображения. Это помогает им в определении форм и фигур, а также позволяет им анализировать связи между различными элементами чертежа.
Кроме того, умение определять количество отрезков на чертеже помогает детям развивать математические навыки, такие как счет, сравнение и классификация. Они могут использовать эти навыки, чтобы решать задачи с числами, сопоставлять и сортировать объекты по их количеству и другим свойствам.
В целом, знание количества отрезков на чертеже не только помогает учащимся подготовиться к изучению более сложных математических концепций в будущем, но и развивает их способности в анализе, логике и пространственном мышлении — навыки, которые будут полезны им не только в учебе, но и в повседневной жизни.
Сколько отрезков на этом чертеже 2 класс?
На чертеже представлены несколько геометрических фигур, включающих отрезки. Чтобы определить количество отрезков на этом чертеже, необходимо внимательно проанализировать каждую фигуру. Все прямые линии, которые имеют начало и конец, можно считать отрезками.
Чтобы их подсчитать, можно воспользоваться следующими шагами:
Проанализировать каждую фигуру на чертеже, обратив внимание на прямые линии.
Определить, есть ли у линий начало и конец.
Если линия имеет начало и конец, считать ее отрезком.
Подсчитать количество отрезков на каждой фигуре.
Сложить количество отрезков на всех фигурах, чтобы получить общее количество отрезков на этом чертеже.
Таким образом, чтобы узнать, сколько отрезков на этом чертеже, необходимо тщательно рассмотреть каждую фигуру и провести подсчет отрезков на каждой из них.
Техники выполнения
Существует два способа выполнения графического диктанта. Первый предполагает, что ребенок внимательно слушает слова педагога и поэтапно строит изображение в тетради. Чтобы повысить интерес крохи к выполнению задания, можно составить текст диктанта в стихотворной форме, дополнить загадками, скороговорками.
Вторая техника – не совсем диктант, поскольку малышу приходится работать самостоятельно. Он может:
- копировать выбранную картинку;
- симметрично дорисовать вторую половинку фигурки;
- «собрать» изображение по инструкции со стрелочками, рисуя линии по клеткам.
Графические диктанты для первоклассников проводят индивидуально и в группе. Иногда их превращают в соревнования – кто быстрее выполнит задание
При выборе условий важно учитывать возраст ребенка. Самым маленьким предлагают простые задания по рисованию звездочек, фруктов, стилизованных животных и рыбок. Мальчишек заинтересуют машинки, девочек – цветочки
Когда принцип работы будет понятен ребенку, можно усложнить задание, предложив нарисовать, например, робота, корабль, слона, замок
Мальчишек заинтересуют машинки, девочек – цветочки. Когда принцип работы будет понятен ребенку, можно усложнить задание, предложив нарисовать, например, робота, корабль, слона, замок.
Пособия для занятий с инструкциями также можно приобрести в книжных магазинах и отделах канцтоваров. Учащихся первого-второго класса заинтересуют развивающие пособия по арифметике О.И. Мельникова. Для дошколенка можно выбрать рабочую тетрадь «Занимательная математика» К.В. Шевелева. Первокласснику стоит приобрести пособие О.А. Холодовой, развивающее познавательные навыки и рассчитанное так, чтобы поддержать школьную программу.