Сравнение чисел со знаками больше, меньше с примерами

Исторический контекст символа примерно

Символ примерно используется в математике для обозначения неравенств и сравнения двух чисел. Он применяется в математических формулах, законах и ответах, чтобы указать, что два значения равны или не равны.

Неравенство представляется через элементы «меньше» или «больше». Например, если нужно записать, что число 1 больше числа 0, мы можем использовать символ примерно, чтобы ответ был 1 > 0. Волнистая черта («меньше») используется для обозначения числа или значения, которое находится на чертами квадратных скобок, например, [0, 1).

Символ примерно также может быть запомнен как «волнистый крокодил», такое название может помочь дошкольникам запомнить его. В математике он используется для сравнения чисел и обозначения неравенства.

Как изображается символ «равно» в математике?

Символ «равно» обозначается горизонтальной чертой «=». Он используется для обозначения равенства двух выражений или чисел. Например, выражение «2 + 3 = 5» означает, что сумма чисел 2 и 3 равна 5. Символ «равно» может быть использован в уравнениях и формулах для указания равенства различных выражений.

Использование символа примерно в математике демонстрируется примерами и ответами. Он может быть использован в формулах и законах, чтобы показать символы «больше» или «меньше», а также для записи значений чисел. Например, 5 > 3, 2 < 4 и 1 = 1 — это примеры использования символа примерно.

В математике символ примерно также может быть использован для записи комбинации символов «больше или равно» (>=) и «меньше или равно» (

Математические ребусы квадрат,

Одна из разновидностей ребусов — магические квадраты. Как их решать? На самом деле совсем не сложно, когда точно понимаешь, что нужно сделать, каковы правила разгадывания и что такого особенного в этих квадратных таблицах.

Чтобы решить магический квадрат нужно заполнить пустые ячейки таким образом, чтобы сумма чисел по любой горизонтали, по любой вертикалям и по диагоналям была одинаковой. В данном случае равнялась сумма чисел должна равняться 9.

Вариант 1

Расшалившиеся монстрики стерли нечаянно цифры в квадрате. Нужно помочь им 
восстановить эти цифры, решив пример на сложение. Так как по горизонтали и 
по вертикали присутствуют не все цифры найдем магическое число, сложив 
цифры по диагонали. 
5 + 3 + 1 = 9 . Значит в пустые ячейки нужно вписать такие цифры, чтобы 
при сложении в разных направлениях получилось 9.
1 столбец:  9 - 3 - 5 = 1
2 столбец:  9 - 3 - 1 = 5
3 столбец: 9 - 5 - 1 = 3
Сделаем проверку решив  примеры таким же образом в линиях.
1 линия: 9 - 3 - 1 = 5
2 линия: 9 - 3 - 5 = 1
3 линия: 9 - 5 - 1 = 3

Вариант 2
Здесь представлено задание посложнее. Требуется расставить цифры в пустые 
ячейки так, чтобы узнать магическое число, благодаря чему и сам квадрат 
станет магическим.
Подсказка: используйте цифры 5, 8, 9, 12, 13, 15. 

Тут уж вряд ли получится найти решение не вооружившись бумагой и ручкой. 
Придется хорошо подумать и подключить воображение.
ОТВЕТ: магическое число = 32. 
А у вас получилось?

Вариант 3
А вот немного другая разновидность квадрата- ребуса. Выполнив несложные 
математические действия, нужно заполнить пустые квадраты цифрами и знаками 
сложения или вычитания. 

Геометрическое изображение

В математике символы часто используются для приближенного графического изображения различных объектов и концепций. Графическое изображение символов позволяет наглядно представить абстрактные идеи и упростить понимание математических понятий.

Один из самых распространенных способов графического изображения символов — использование знаков и символов для представления различных математических функций, операций и выражений.

Например, операция сложения часто изображается с помощью символа «+» в геометрических приближениях. При этом, всякий раз, когда нужно выполнить сложение, мы видим символ «+» в графике или на рисунке.

Также широко используются графические изображения для функций. Например, функция y = x^2 можно приближенно изобразить с помощью графика параболы, где ось x является горизонтальной осью, ось y — вертикальной осью, а точки на графике представляют значения функции в различных точках.

В некоторых случаях графическое изображение символов может быть представлено с помощью таблиц и списков. Например, для представления числовых данных, таких как координаты точек, можно использовать таблицы или списки, где каждая строка соответствует одной точке, а каждый столбец — одной измеренной величине.

Геометрическое изображение символов в математике играет важную роль в упрощении и объяснении математических концепций. Оно позволяет лучше визуализировать и понять сложные идеи, а также использовать графические методы для решения задач и анализа данных.

Графическое представление

В математике символы и выражения могут быть представлены графическими образами. Графическое представление помогает наглядно проиллюстрировать концепции и связи между символами и выражениями.

Знаки математических операций, такие как плюс (+), минус (-), умножение (×) и деление (÷), могут быть изображены графически для наглядности. Например, знак плюс (+) представляется горизонтальной линией, пересеченной вертикальной линией в центре. Знак минус (-) представляется горизонтальной линией без вертикальной линии в центре.

Также графическое представление может быть использовано для обозначения скобок в математических выражениях. Скобки могут быть изображены графически в виде круглых скобок (), квадратных скобок [] или фигурных скобок {}. Они используются для группировки выражений и указания приоритета операций.

Графическое представление может быть использовано для приближенного изображения графиков функций. График функции представляет собой изображение, которое отображает зависимость значения функции от значения ее аргумента. График функции может быть изображен в виде линий, кривых или точек на координатной плоскости.

Также операции и символы математики могут быть представлены с помощью таблиц. Таблицы могут использоваться для отображения числовых значений, формул или других связанных данных. Они могут быть организованы в виде строк и столбцов для удобства чтения и понимания информации.

Графическое представление в математике помогает визуализировать абстрактные идеи и сделать их более доступными для понимания и использования.

Изображение на плоскости

В математике символы и знаки играют важную роль при рассмотрении различных объектов и операций. Часто эти символы изображаются на плоскости с помощью различных приближений и графических представлений.

Возьмем, например, скобки. Они используются для обозначения группировки операций или выражений. Левая скобка «(» показывает начало группировки, а правая скобка «)» показывает ее конец. Эти символы обычно изображаются параллельными линиями на плоскости.

Также в математике очень важны функции и их графики. Функция — это связь между двумя переменными, в которой каждому элементу одного множества (аргументу) сопоставляется элемент другого множества (значению). График функции — это геометрическое представление функции на плоскости, где на одной оси откладываются значения аргумента, а на другой оси — значения функции.

Операции также могут быть изображены на плоскости. Например, сложение чисел может быть представлено с помощью отрезка, где начало отрезка показывает первое число, а конец отрезка — второе число. При сложении этих чисел получается отрезок, начало которого соответствует началу первого отрезка, а конец — концу второго отрезка.

Таким образом, изображение символов и операций на плоскости в математике позволяет наглядно представить различные математические понятия и связи между ними.

Расположение знака приблизительно на клавиатуре

Знак приблизительно (~) можно найти на клавиатуре, нажав клавишу Shift и клавишу `, которая обычно расположена над клавишей Tab.

Однако, в некоторых раскладках клавиатуры (например, в английской раскладке), знак приблизительно находится на другой клавише. Например, в английской раскладке знак приблизительно расположен на клавише \, которую можно найти слева от правого Shift.

Знак приблизительно (~) используется для обозначения приблизительного значения, или для сравнения двух величин. Например, 2+2 ~ 4 означает, что 2 плюс 2 приблизительно равно 4.

Клавиша	Расположение знака приблизительно
`	Shift + `
\	Shift + \

Итак, чтобы найти знак приблизительно на клавиатуре, следует нажать сочетание клавиш Shift и соответствующей клавиши ( ` или \ ) в зависимости от раскладки клавиатуры.

Как изображается символ примерно в математике

В математике символы используются для обозначения различных математических объектов, операций и связей. Они помогают структурировать и представлять информацию в виде формул, выражений, уравнений и графиков.

Математические символы могут представлять операции, такие как сложение (+), вычитание (-), умножение (×), деление (÷), возведение в степень (^), извлечение корня (√) и другие.

Символы могут представлять функции, такие как синус (sin), косинус (cos), тангенс (tan), логарифм (log) и другие. Они обычно указываются в виде букв или сокращений этих функций.

Математические символы также могут обозначать скобки, которые используются для группировки выражений и определения порядка операций. Примерами таких символов могут быть круглые скобки ( ), квадратные скобки , фигурные скобки { } и другие.

Графики и диаграммы в математике могут использовать символы для обозначения различных точек, линий, кривых и областей. Они могут сконструироваться из базовых геометрических форм, таких как отрезки, окружности, эллипсы и другие.

Приближение в математике также может быть обозначено символами. Например, символы «≈» или «~» могут указывать на приближенное равенство двух чисел или выражений.

Символы могут использоваться для обозначения переменных, констант и параметров в выражениях и уравнениях. Они могут быть представлены как буквенные символы, цифры или специальные обозначения.

Примеры символов в математике

Символ
Обозначение
Описание

+
Сложение
Символ обозначает операцию сложения двух чисел или выражений

*
Умножение
Символ обозначает операцию умножения двух чисел или выражений

sin
Синус
Символ обозначает тригонометрическую функцию синус

( )
Круглые скобки
Символы обозначают группировку и приоритет операций

≈
Приближение
Символ обозначает приближенное равенство двух чисел или выражений

x
Переменная
Символ обозначает неизвестную или изменяющуюся величину в выражениях и уравнениях

Примеры использования знака равенства

В математике знак равенства показывает, что значения двух выражений или чисел (слева и справа от знака) равны. Например, уравнение 2 + 3 = 5 показывает, что сумма чисел 2 и 3 равна 5.

Одним из дополнительных символов, которые могут быть использованы вместе с знаком равенства, является символ меньше (

В программировании знак равенства также используется для присваивания значений переменным. Например, код x = 10 присваивает переменной x значение 10.

Знак равенства можно комбинировать с другими символами, чтобы показать более сложные отношения. Например, символ «больше» (>) может быть использован вместе с знаком равенства для показа, что одно значение больше или равно другому.

Окружности

Итак, с правильными многоугольниками мы разобрались. А что у нас с окружностями? Точки, лежащие на одной окружности называются конциклическими. Очевидно, что нет никаких проблем нарисовать какие угодно окружности, проходящие через два или три узла решётки. А что насчёт ровно четырёх, пяти или шести конциклических точек?

Существует теорема Шинцеля, которая утверждает, что для любого натурального можно построить окружность, проходящую ровно черезузлов решётки. Статья, в которой Андрэ Шинцель приводит своё доказательство занимает чуть больше страницы и представляет образец красивой математики. Но я не хочу развивать здесь эту тему, поскольку, центры этих окружностей не попадают на решётку и их в геометрии решётки, которую мы сейчас рассматриваем, как бы, не существуют.

Оригинальная статья Андрэ Шинцеля.

Давайте вместо этого зададимся вопросом а через сколько узлов может проходить окружность с центром в узле решётки?

Здесь опять имеет смысл обратиться к гауссовым числам. Пусть наша окружность с радиусом имеет центр в точке 0 и проходит через точку , а значит, . Мы уже знаем, что у каждого гауссова числа есть три ассоциированных с ним числа и . И все они имеют одинаковую норму. Это значит, если наша окружность проходит через один узел, то она обязана проходить ещё через три узла, ассоциированные с ним. Это сразу приводит к тому, что любая окружность с центром на решётке проходит через число точек, кратное четырём.

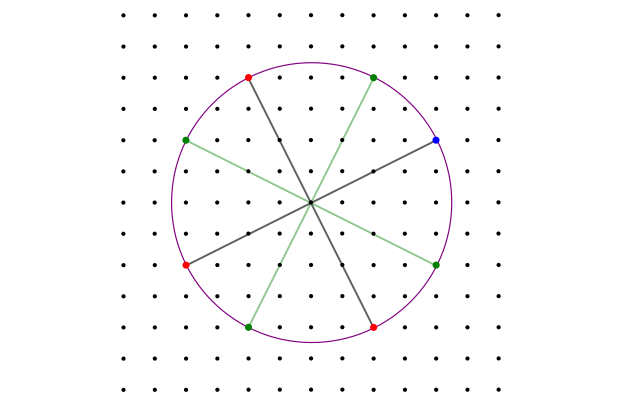Ассоциированные (красные) и сопряжённые (зелёные) узлы для узла, выделенного синим цветом.

Кроме ассоциированных у гауссовых чисел есть ещё и сопряжённые числа, имеющие такую же норму. Для числа сопряжённым будет . И если узел, лежащий на окружности не соответствует вещественному числу, то кроме ассоциированных к нему добавятся ещё и сопряжённые с ними узлы. Таким образом, у любого узла, не лежащего на вещественной или мнимой осях, есть как минимум семь конциклических узлов. Однако, их может быть и больше.

Мы уже встречали числа, имеющие более одного представления в виде суммы двух квадратов, такие, как 25 или 100. Зная простые делители некоторого числа , можно определить количество способов разложить его в виде такой суммы. Все делители можно разбить на две группы: делящиеся на гауссовы простые числа, не делящиеся на них. Первые не имеют разложения в виде суммы квадратов, вторые — имеют. При этом, в следствие упомянутого тождества Брахмагупты-Фибоначчи, произведение сумм квадратов само является суммой квадратов. Таким образом получается число возможных комбинаций из двух квадратов (либо соответствующих им гауссовых чисел), дающих в сумме число

где и обозначают количество делителей числа , дающих, соответственно 1 и 3 в остатке при делении на 4. Ниже приведена диаграмма точек на квадратной регулярной решётке, на которой размер узла отражает число точек, конциклических с этим узлом.

А вот похожая и даже, как кажется более простая Проблема круга Гаусса о количестве узлов решётки, попадающих внутрь круга заданного радиуса с центром в узле, до сих пор не решена.

С решётками связаны многие задачи теории чисел и теории колец. Мы рассмотрели те из них, что с одной стороны, будут понятны школьникам, а с другой достаточно интересны, чтобы превратиться в исследования и дать тем же школьникам почувствовать себя крутыми.

Предыдущие статьи серии Математическая продлёнка:

Различные заметки и материалы на Дзен-канале Онлайн-кружок математики .

Правила использования знака примерно

Правильное использование знака примерно – это важный аспект научной и технической деятельности. Он используется для указания приблизительной величины, значения, времени и расстояния. Данный знак представляет из себя знак тильды ~ и обязательно ставится вместе с числом или словом.

При использовании знака примерно нужно помнить, что он не является точным значением, а лишь предполагаемым. Например, если приблизительное значение равно 5, то это может значит 4, 6 или любое другое значение в зависимости от контекста и способа округления.

Для более точного использования знака примерно можно использовать числовые диапазоны. Например, если нужно указать примерное время выполнения задания, то можно написать: 20-30 минут ~. Также можно использовать знаки «не менее» или «не более» в комбинации с знаком примерно для более точного определения величины.

Не стоит злоупотреблять знаком примерно и ставить его везде, где возможно.
Важно убедиться в корректности использования знака примерно.
Необходимо быть внимательным и не ошибаться в расстановке знака примерно, т.к. это может привести к неправильному пониманию значения.. В целом, знак примерно – это инструмент, который помогает указать приблизительный характер измеряемой величины, указать диапазон или приблизительный временной интервал

Важно уметь его использовать правильно, чтобы избежать недопонимания и ошибок при выполнении научных и технических работ

В целом, знак примерно – это инструмент, который помогает указать приблизительный характер измеряемой величины, указать диапазон или приблизительный временной интервал

Важно уметь его использовать правильно, чтобы избежать недопонимания и ошибок при выполнении научных и технических работ

Общая алгебра

Символ TeX (Команда TeX)	Символ (Юникод)	Название	Значение	Пример
Произношение
\displaystyle{ \triangleleft }	⊲	Нормальная подгруппа, идеал кольца	\displaystyle{ H \triangleleft G } означает «\displaystyle{ H } является нормальной подгруппой группы \displaystyle{ G }», если \displaystyle{ G } — группа, и «\displaystyle{ H } является (двусторонним) идеалом кольца \displaystyle{ G }», если \displaystyle{ G } — кольцо.
«нормальна в», «… является идеалом …»
\displaystyle{ }		Индекс подгруппы, размерность поля	\displaystyle{ } означает «индекс подгруппы \displaystyle{ H } в группе \displaystyle{ G }», если \displaystyle{ G } — группа, и «размерность поля \displaystyle{ H } над полем \displaystyle{ G }», если \displaystyle{ G } и \displaystyle{ H } — поля.
«индекс … в …», «размерность … над …»
\displaystyle{ \times }	×	Прямое произведение групп	\displaystyle{ G \times H } означает «прямое произведение групп \displaystyle{ G } и \displaystyle{ H }».
«прямое произведение … и …»
\displaystyle{ \oplus }	⊕	Прямая сумма подпространств	\displaystyle{ V = V_1 \oplus V_2 } означает «пространство \displaystyle{ V } разлагается в прямую сумму подпространств \displaystyle{ V_1 } и \displaystyle{ V_2 }».
«прямая сумма … и …»
\displaystyle{ }		элементов группы	\displaystyle{ } означает «коммутатор элементов \displaystyle{ g } и \displaystyle{ h } группы \displaystyle{ G }», то есть элемент \displaystyle{ ghg^{-1}h^{-1} }.
«коммутатор … и …»
\displaystyle{ G^\prime }	G’		\displaystyle{ G^\prime } означает «коммутант группы \displaystyle{ G }».
«коммутант …»
\displaystyle{ \langle\ \rangle_n }	⟨ ⟩n		\displaystyle{ \langle a\rangle_n } означает «циклическая группа порядка \displaystyle{ n }, порождённая элементом \displaystyle{ a }».
«Циклическая группа порядка \displaystyle{ n }, порождённая \displaystyle{ a }»
\displaystyle{ * }	*	Мультипликативная группа поля	\displaystyle{ F^{*} } означает «мультипликативная группа поля \displaystyle{ F }», если \displaystyle{ F } — поле.
«мультипликативная группа …»

Расположение знака приблизительно на мобильной клавиатуре

На мобильной клавиатуре расположение знака «приблизительно равно» может зависеть от операционной системы и типа устройства. Однако, в большинстве случаев он находится в нижнем регистре клавиатуры на одной из дополнительных вкладок, к которой можно переключиться с помощью символа «123» или стрелки влево.

Для того чтобы найти знак «приблизительно равно», нужно открыть клавиатуру и прокрутить набор символов, включая числа и операторы, с помощью полосы прокрутки или жестов, пока не найдете нужный символ. Он выглядит как знак равенства «равно», только вместо двух горизонтальных черток имеет одну, но с небольшим вертикальным отклонением вверх.

Пример:

Если воспользуемся числовой клавиатурой, то находим минус (-) справа от единицы (1). Затем, двигаясь влево, можно найти знак приблизительно равно (≈).

Важно отметить, что в разных мобильных устройствах и операционных системах расположение символа может отличаться. Если вы не можете найти знак «приблизительно равно» на вашей мобильной клавиатуре, попробуйте воспользоваться символами, которые похожи на «приблизительно равно», такие как «≈» или «~»

Клавиша символов

На клавиатуре найти знак приблизительно примерно равно можно с помощью клавиши символов. Этот знак обычно обозначается как «~» и располагается на клавише, справа от цифры «1».

Клавиша символов также может содержать другие полезные символы. Например, знак равно («=»), знак плюс («+»), знак минус («-«) и т. д. Они все находятся на клавише символов и доступны при нажатии клавиши с символом «~».

Эта клавиша полезна, когда вы работаете с программами, где нужно указывать значения, приблизительно равные друг другу. Например, при задании численных интервалов или диапазонов.

Итак, если вам нужен знак приблизительно примерно равно, не забудьте заглянуть на клавишу символов!

Дополнительные варианты для поиска

Помимо знака «приблизительно равно» (~), на клавиатуре можно также найти несколько других вариантов для обозначения примерной равности в математических выражениях.

К примеру, одним из таких вариантов является знак «только почти равно» (≈). В отличие от знака «~», знак «≈» используется, чтобы показать, что два значения или выражения почти равны, но не совсем.

Еще одним вариантом является знак «равно с минусом» (≡). Он используется, чтобы указать на точное равенство между двумя выражениями, которые являются эквивалентными или идентичными.

Кроме того, некоторым людям может быть удобно использовать знак «единица приблизительно равна» (≈), чтобы показать, что значение равно приблизительно 1.

Все эти знаки могут быть полезны при записи математических выражений и формул, где требуется указать примерную равность или точное эквивалентное значение.

Символы линейной алгебры

Символ	Название символа	Значение / определение	пример
·	точка	скалярное произведение	а · б
×	пересекать	векторный продукт	а × б
А ⊗ Б	тензорное произведение	тензорное произведение A и B	А ⊗ Б
	внутренний продукт
[]	кронштейны	матрица чисел
()	круглые скобки	матрица чисел
| А |	детерминант	определитель матрицы A
det ( А )	детерминант	определитель матрицы A
|| х ||	двойные вертикальные полосы	норма
А Т	транспонировать	матрица транспонировать	( A T ) ij = ( A ) ji
A †	Эрмитова матрица	матрица сопряженная транспонировать	( A † ) ij = ( A ) ji
А *	Эрмитова матрица	матрица сопряженная транспонировать	( A * ) ij = ( A ) ji
А -1	обратная матрица	AA -1 = I
ранг ( А )	ранг матрицы	ранг матрицы A	ранг ( А ) = 3
тусклый ( U )	измерение	размерность матрицы A	dim ( U ) = 3

Значение знака примерно

Знак примерно используется для указания приблизительности числа или количества. Он обычно обозначается знаком тильда (~) или словом «примерно». Например, «Этот груз весит примерно 100 килограммов».

Знак примерно помогает избежать точного указания числа, когда необходимо указать примерную величину, которая может варьироваться в зависимости от условий.

Его использование особенно полезно при описании активности или процесса, который не может быть точно измерен. Например, «Примерно 80% населения города пользуется общественным транспортом».

Важно помнить, что значение знака примерно не является точным и может быть недостаточным в контексте, требующем более точной оценки. В таких случаях, использование дополнительных методов измерения и оценки может помочь дать точный ответ

• Знак примерно может также быть использован в математике для описания примерного результата вычислений.
• В некоторых случаях, знак примерно может быть заменен на другие слова, такие как «около», «близко к», «в пределах».

Корректное использование знака примерно помогает избежать недоразумений и обеспечивает точность в коммуникации.

Линейная алгебра

Символ TeX (Команда TeX)	Символ (Юникод)	Название	Значение	Пример
Произношение
\displaystyle{ \otimes }	⊗	Тензорное произведение	\displaystyle{ T_1 \otimes T_2 } означает «тензорное произведение тензоров \displaystyle{ T_1 } и \displaystyle{ T_2 }».
«тензорное произведение … и …»
\displaystyle{ A^T }	AT	Транспонированная матрица	\displaystyle{ A^T } означает «транспонированная матрица \displaystyle{ A }».
«транспонированная матрица …»
\displaystyle{ E_{i,\,j} }	Ei, j	Матричная единица	\displaystyle{ E_{i,\,j} } означает «матричная \displaystyle{ i,\;j }-единица», то есть матрица, у которой на месте \displaystyle{ (i,\;j) } стоит единица, а на остальных местах — нули.
«матричная единица …»
\displaystyle{ * }	*	Сопряжённый оператор	\displaystyle{ \mathcal{A}^{*} } означает «линейный оператор, сопряжённый к \displaystyle{ \mathcal A }», если \displaystyle{ \mathcal A } — линейный оператор. \displaystyle{ V^{*} } означает «линейное пространство, сопряжённое к \displaystyle{ V } (дуальное к \displaystyle{ V })», если \displaystyle{ V } — линейное пространство.
«оператор, сопряжённый к …»; «пространство, сопряжённое к …»;

Способы как набрать знак примерно (приблизительно) на клавиатуре

В жизни бывают разные ситуации, поэтому чем больше способов вы знаете, тем лучше. Как говорится, альтернатива никогда не будет лишней. Кстати, обзор в тему зачем нужны аналоги. Возвращаясь к сути, вот, собственно, несколько способов как набрать знак приблизительно (примерно) на клавиатуре.

Метод 1. Скопируйте знак примерно (приблизительно)

Зачем ждать? Если вам нужен символ, то самое простое и очевидное это просто скопировать его. Собственно, к тому как это сделать и переходим.

Вот знак примерно (приблизительно): ≈

Метод 2. Знак примерно (приблизительно) с помощью комбинаций на клавиатуре

Сразу отмечу, что данный способ далеко не везде и всегда приводит к нужному результату. И вот что нужно сделать.

Чтобы набрать знак приблизительно (примерно), вам нужно зажать клавишу «Alt» и набрать «008776» или просто «8776» (в правой колодке клавиатуры). Должен появиться знак «≈».

Метод 3. Знак примерно (приблизительно) с помощью таблицы символов Windows

Знак примерно (приблизительно) можно набрать и с помощью классного инструмента Windows под названием Таблица символов, который позволяет найти нужный символ или знак. И вот что нужно делать:

1. Откройте меню Пуск и в поиске наберите «таблица символов».

2. Выберите пункт с одноименным названием.

3. Откроется окно с символами.

3.1. В нем можно либо вручную найти знак «примерно» — «≈».

3.2. Либо можно сделать следующее.

3.2.1. Установите галочку напротив пункта «Дополнительные параметры».

3.2.2. Внизу в выпадающем списке «Группировка» выберите пункт «Диапазоны Юникода».

3.2.3. Откроется небольшое окно, в нем необходимо выбрать пункт «Математические операторы».

3.2.4. Теперь щелкните по знаку приблизительно «≈». Затем нажмите кнопку «Выбрать» под таблицей и скопируйте символ из текстового поля рядом (или нажмите кнопку «копировать»).

3.2.5. Дальше вставьте знак «примерно» там, где вам необходимо.

Метод 4. Еще можно схитрить и набрать символ, похожий на знак примерно (приблизительно)

Смекалка это полезная вещь! К ней всегда стоит прибегать. Чего я сейчас и сделаю. На клавиатуре слева от кнопки «1» существует кнопка с символом «ё» в русской раскладке. В латинице это специфическая верхняя запятая — `. Если перевести раскладку в латиницу, одновременно нажать Shift и эту кнопку, то получится символ «тильда» — «~», который отчасти похож на символ приблизительно. Вполне неплохой вариант для случаев, когда нужно быстро передать смысл.

Метод 5. Коды знака приблизительно (примерно) в html

А вот еще один метод на тот случай, если вам нужно набрать знак примерно в html. Скажем, в случае, когда вы пишите формулы. Соответственно вот сами коды.

Чтобы вставить знак примерно (приблизительно): &#8776; и &asymp;

• Что такое Тема для сайта простыми словами?
• Размеры форматов бумаги